J'ai besoin de connaître pour cet exercice :

Les techniques de factorisation et de développement
la particularité des identités remarquables
Les équations produits
Le remplacement des x par des valeurs dans une expression

 

Je revois les fiches correspondantes :

Le développement
La factorisation
Les identités remarquables
Les équations à une inconnue

Calcul avec des x ;

+ éventuellement les bases de calcul

Remarque : si je regarde les corrigés d'annales précédents, (1 et 2), je remarque que ce type d'exercice est toujours demandé dans les sujets de brevet....

---

A=(x -2)²+(x - 2)(3x +1)

1. Je développe et réduis A :

Développer c'est effectuer tous les calculs demandés dans l'expression

A=(x -2)²+(x - 2)(3x +1)

Les puissances sont prioritaires : je vais d'abord effectuer :
(x -2)²

J'ai un carré qui se distribue sur une parenthèse, que je ne peux pas calculer : cela me fait penser à une identité remarquable : de quel type ?? (a - b)²

Et quel est le développement de cette identité ?

(a - b)² = a² - 2 x a x b + b²

Dans ma parenthèse : a = x et b = 2 : j'applique donc la formule à ces termes :

(x)² = x x x = x²
2 x x x 2 = 2 x x 2 = 4x
2 ² = 2 x 2 = 4

Mon expression devient :

A = (x² - 4x + 4) +(x - 2)(3x +1)

J'ai maintenant une multiplication : elle est prioritaire :
(x - 2)(3x +1)

J'applique pour cela la distributivité de la multiplication :
(x - 2) x (3x +1) = x x 3x + x x 1 - 2 x 3x - 2 x 1
x x 3x = 3x²
x x 1 = x
- 2 x 3x = - 6x
- 2 x 1 = - 2
(x - 2) x (3x +1) = = 3x² + x - 6x - 2
+ x - 6x = - 5x
(x - 2) x (3x +1) = 3x² - 5x - 2

Je restitue le résultat de ma multiplication dans mon expression :

A = (x² - 4x + 4) +( 3x² - 5x - 2)

J'enlève maintenant les parenthèses :
Je n'ai pas de signe - devant, donc aucun problème !!

A = x² - 4x + 4 + 3x² - 5x - 2

Il ne me reste plus qu'à calculer les termes de même nature ensemble
x² + 3x² = 4x²
- 4x - 5x = - 9x
4 - 2 = 2

A = 4x² - 9x + 2

Mon expression est développée, réduite et ordonnée (ordre : termes en x², termes en x , et nombres entiers)

---

2. Je factorise A :
Je reprends mon expression de départ : A = (x -2)²+(x - 2)(3x +1)

Mon expression est-elle prête à être factorisée ?? C'est à dire sous la forme :
......x .......+/-....... x ......

Apparemment non : je vais donc la modifier pour qu'elle le devienne
Je sais que (x -2) ² = (x -2) x (x -2)

Je peux écrire :
A = (x -2) x (x -2) +(x - 2)(3x +1)

Mais mon expression n'est toujours pas de la forme :......x .......+/-....... x ......
Je peux donc écrire : (x - 2)(3x +1) = (x - 2) x (3x +1) ; j'obtiens ainsi une expression correctement structurée :

(x -2) x (x -2) + (x - 2) x (3x +1)

Je cherche alors à faire apparaître le facteur commun aux 2 expressions multipliées :
Il est parfaitement visible : il s'agit de (x -2)

(x -2) x (x -2) + (x - 2) x (3x +1)

Je le sors et le multiplie par tout le reste :
(x - 2) x ............

Que me reste-t-il ??
(x -2) + (3x +1)

Je calcule :
(x -2) + (3x +1)
= x -2 + 3x +1
= x + 3x - 2 + 1
x + 3x = 4x
- 2 + 1 = - 1
(x -2) + (3x +1) = 4x - 1

A = (x -2) x (4x - 1)

A = (x -2) (4x - 1) ; mon expression est factorisée

---

3. Je dois résoudre l'équation : (x -2) (4x - 1) = 0

Cette équation n'a plus rien à voir avec mon expression Aet pourtant !!

Je regarde attentivement tous les calculs que j'ai déjà effectués dans cet exercice, et m'aperçois que (x -2) (4x - 1) n'est rien d'autre que le résultat de la factorisation de A : ouf !! Cela me rassure : je dois être sur la bonne voie (sans doute, ma factorisation sera juste)

Je dois maintenant résoudre une équation : cela veut dire quoi ?? Et bien résoudre une équation, c'est trouver la valeur de x dans une expression donnée

Ici : je dois donner la valeur de x pour que (x -2) (4x - 1) soit égal à 0

Je suis ici en équation produit :

(x -2) (4x - 1) est une multiplication (x -2) x (4x - 1): DONC

Si (x -2) = 0 , (x -2) (4x - 1) sera forcément égal à 0
Et si (4x - 1) = 0 , (x -2) (4x - 1) sera forcément égal à 0

J'aurai donc 2 solutions pour la valeur de x

Pour que (x -2) soit égal à 0 il faut que : x -2 = 0 x = 2

Pour que (4x - 1) soit égal à 0 il faut que : 4x - 1 = 0 4x = 1 x =

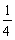
S = [ 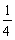; 2 ]

---

4. Enfin, je dois calculer A pour
Qu'est-ce que cela signifie ?? Et bien que je devrai remplacer x par la valeur dans mon expression :

Je choisis pour cela la forme de l'expression qui me paraît la plus simple :

• Forme initiale : A=(x -2)²+(x - 2)(3x +1)
• Forme développée : A = 4x² - 9x + 2
• Forme factorisée : A = (x -2) (4x - 1)

Je choisis celle qui me semble la plus pratique pour la fraction = la forme factorisée
A = (x -2) (4x - 1)
A = ( -2) (4 x - 1)
Je calcule les parenthèses :
( - 2) = ( - ) = -
(4 x - 1) = - 1 = 2 - 1 = 1
Je me retrouve avec :
A = (- ) (1)
A = (- ) x (1)
A = -
C'est le résultat de mon expression pour x =
Fin de l'exercice : j'espère que vous commencez vraiment à vous familiariser à ce genre d'exercice : car c'est l'exercice "type" du brevet par excellence !!