J'ai besoin de connaître pour cet
exercice :
Les techniques de
factorisation et de développement
la particularité des identités
remarquables
Les équations produits
Je revois les fiches
correspondantes :
Le développement
La factorisation
Les identités
remarquables
Les équations à une
inconnue
+ éventuellement : calcul avec des x
; et les bases de calcul
E = 4x2
- 9 + (2x +
3) ( x - 1)
1. Je
factorise : 4x2 - 9
Mon expression est-elle prête à être
factorisée ?? C'est à dire sous la forme :
......x .......+/-....... x ......
Apparemment non : je vais donc la modifier pour qu'elle le
devienne
4 x x2
- 3 x 3
Mon expression est maintenant correctement structurée
: je cherche à faire apparaître le facteur
commun aux 2 expressions multipliées :
Il n'y en a pas : en effet, rien de commun dans 4 et 3 (ou
même 9), et pas de x dans la
2ème multiplication
Seule solution : les identités remarquables
Mon expression serait une identité remarquable
développée ??
Je regarde laquelle parmi les 3 proposées : (voir
fiche)
4x2 - 9 =
ressemble d'avantage à a2 -
b2
Il me reste à trouver a et b
a = 2x (car 2x x
2x = 4x2 ; le
carré se distribue sur les 2 termes)
b = 3 (car 32 = 9 ou
9 = 3)
J'ai trouvé mes a et b : je peux donc donner la
factorisation correspondante :
a2 -
b2 = (a + b) x (a - b)
Donc la factorisation de
4x2 - 9 est
:
(2 x + 3) x
(2x - 3)
Deuxième partie de la question : je dois utiliser ce
résultat pour factoriser E
E = 4x2
- 9 + (2x +
3) ( x - 1)
DONC
E = (2 x
+ 3) x (2 x - 3) +
(2x + 3) ( x - 1)
Je factorise : en réécrivant l'expression pour
qu'elle soit sous la forme :
...... x .......+/- ........ x .......
E = (2x
+ 3) x (2x - 3) +
(2x + 3) x ( x - 1)
Je recherche le facteur commun aux deux expressions
multipliées : (2x + 3)
Je le sors et le multiplie par tout le reste :
(2x + 3) x
............
Que me reste-t-il ??
(2x - 3) + (
x - 1)
Je calcule :
(2x - 3) + (
x - 1)
= 2x - 3 +
x - 1
= 2x + x
- 3 - 1
2x + x =
3x
- 3 - 1 = - 4
(2x - 3) + (
x - 1) = 3x - 4
E = (2x
+ 3) x (3x -
4)
E = (2x
+ 3) (3x -
4) ; mon expression est factorisée
E = 4x2
- 9 + (2x +
3) ( x - 1)
2. Je développe
E :
Développer c'est effectuer tous les calculs
demandés dans l'expression
E = 4x2
- 9 + (2x +
3) ( x - 1)
La multiplication est prioritaire : je dois donc effectuer
d'abord:
(2x + 3) ( x - 1)
J'applique pour cela la distributivité de la
multiplication :
(2x + 3) x ( x - 1) =
2x x x
- 2x x 1 + 3 x
x - 3 x 1
2x x x
= 2x2
2x x
1 = 2x
3 x x =
3x
3 x 1 = 3
(2x + 3) x ( x - 1) =
2x2 - 2x +
3x - 3
- 2x
+ 3x =
x
(2x + 3) x (
x - 1) = 2x2
+ x - 3
Je restitue le résultat de ma multiplication dans mon
expression :
E = 4x2
- 9 + (2x2 +
x -
3)
J'enlève la
parenthèse : je ne change rien car j'ai un signe +
devant la parenthèse
E = 4x2
- 9 + 2x2 +
x -
3
Je calcule les termes de même nature ensemble
4x2 +
2x2 =
6x2
- 9 - 3 = - 12
E = 6x2
+ x - 12
Mon résultat est ordonné ; je ne peux plus
rien calculer (il est donc aussi réduit)
E = 6x2 +
x -
12
C'est le résultat final de mon
développement
3. Je dois résoudre l'équation :
(2x + 3)
(3x - 4) = 0
Cette équation n'a plus rien à voir avec mon
expression E et pourtant !!
Je regarde attentivement tous les calculs que j'ai
déjà effectués dans cet exercice, et
m'aperçois que (2x
+ 3) (3x -
4) n'est rien d'autre que le résultat de la
factorisation de E : ouf !! Cela me rassure : je dois
être sur la bonne voie (sans doute, ma factorisation
sera juste)
Je dois maintenant résoudre une équation :
cela veut dire quoi ?? Et bien résoudre une
équation, c'est trouver la valeur de x
dans une expression donnée
Ici : je dois donner la valeur de x
pour que (2x
+ 3) (3x -
4) soit égal à 0
Je suis ici en équation produit :
(2x + 3)
(3x - 4) est une multiplication : DONC
Si (2x
+ 3) = 0 (2x + 3)
(3x - 4) sera forcément égal
à 0
Et si (3x - 4) = 0 (2x
+ 3) (3x -
4) sera forcément égal à 0
J'aurai donc 2 solutions pour la valeur de x
|
Pour que
2x
+ 3 soit
égal à 0 il faut que :
2x
+ 3 = 0
2x
= - 3
x
= -
|
Pour que
3x
- 4 soit
égal à 0 il faut que :
3x
- 4 = 0
3x
= 4
x
= 
|
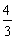
S = [ - ;
]
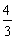