J'ai besoin de connaître pour cet
exercice :
Les
propriétés des opérations et des
fractions :
Les propriétés de calcul avec des
puissances
Les opérations avec des racines
carrées
Je revois les fiches correspondantes :
Les bases de calcul
Les fractions
Les puissances
Les racines carrées
1/
A= 
-
÷ 
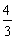Propriété : J'ai une soustraction et une
division de fractions : je commence par la division, qui est
prioritaire :
÷
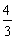Règle : pour diviser un nombre par une fraction, je
dois multiplier ce nombre par l'inverse de cette fraction
:
Ici je dois divise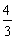r par
: je vais donc multiplier 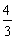par
l'inverse de
Inverse de = 
Ma division devient : 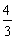x
Je peux alors calculer normalement ma multiplication : je
dois pour cela multiplier ensemble les numérateurs et
les dénominateurs :
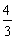x =
J'essaie toujours de simplifier au maximum avant de calculer
:
=
=
=
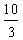
Mon expression A devient alors :
A = -
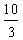
Je suis en soustraction de fractions : pour additionner ou
soustraire 2 fractions, je dois d'abord les mettre sous le
même dénominateur :
Je regarde les dénominateurs de mon expression : 3 et
3
Cela tombe bien : le dénominateur est le même
:
Il ne me reste alors plus qu'à soustraire ensemble
les numérateurs :
Règle : Pour additionner ou soustraire deux
fractions de même dénominateur, il me suffit
d'additionner ou soustraire leurs numérateurs :
- =
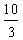7 - 10 = - 3
- = -
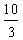= 1
donc -= - 1
Mon opération est terminée :
A = -
1
2/
B = - 42 + 103 x
10-1 + (-3)2
Les puissances : =
Règle : Un nombre soumis à une puissance (ou
exposant) se multiplie par lui même, autant de fois
que l'indique la puissance (ou exposant)
J'applique cette règle :
42 = 4 x 4 = 16
103 =
10 x 10 x 10 =
1000
10-1 =
1/101 = 1 :
10 = 0,1 (j'appliqua la règle des puissances
négatives: a- n = 1/
an)
(-3)2 =
(-3) x (-3) = 9
Mon expression devient alors :
B = - 16 + 1000 x 0,1 + 9
J'ai une multiplication : je sais qu'elle est prioritaire
par rapport à tout le reste : je l'effectue
1000 x 0,1 = 100
B = - 16 + 100 + 9
Il ne me reste plus alors qu'à calculer :
B = - 16 + 100 + 9
100 + 9 = 109 ; 109 - 16 = 93
B =
93
Je vérifie ma réponse : mon résultat
doit être sous la forme décimale (nombre
à virgule) ; or, il apparaît que le
résultat est un nombre entier : y aurait-il une
erreur ??
3/
C = 2
27 - 43 +
12
Règle : je suis en addition et soustraction de
racines carrées : je sais que je ne peux ni
additionner ni soustraire 2 racines carrées, si elles
n'ont pas le même radical (racidal = nombre sous la
racine carrée)
Je ne peux donc rien faire pour le moment avec l'expression
C à moins de trouver des racines carrées
communes, après simplification
Je dois donc commencer par essayer de simplifier les racines
carrées, chacune séparément : pour cela
je les décompose
:
Décomposition de 27
= 3 x 9
= 3 x9
Est-ce que je connais la racine carrée de 3 ? NON ;
je ne connais aucun nombre, qui, multiplié par
lui-même, donne 3 : je laisse donc 3 sous
sa forme racine carrée
Est-ce que je connais la racine carrée de 9 ? OUI =
9 = 3 car 32 = 9
Je peux donc écrire :
27 = 3 x3
Décomposition de 3
= Est-ce que je connais la
racine carrée de 3 ? NON ; je ne connais aucun
nombre, qui, multiplié par lui-même, donne 3 :
je laisse donc 3
Décomposition de 12
= 3 x 4
= 3 x4
Est-ce que je connais la racine carrée de 3 ? NON ;
je ne connais aucun nombre, qui, multiplié par
lui-même, donne 3 : je laisse donc 3 sous
sa forme racine carrée
Est-ce que je connais la racine carrée de 4 ? OUI =
4 = 2 car 22 = 4
Je peux donc écrire :
12 = 2 x3
Mon expression devient alors :
C = 2 (3 x3) - 4 3 + 2
x3
C = 6 3 - 4 3 + 2
3
Et oh surprise : grâce à la
décomposition de mes racines, je retombe sur une
expression avec des racines carrées qui ont toutes le
même radical : 3
Je sais que je peux donc les additionner et les soustraire,
en ajoutant ou retranchant le nombre de racines
carrées :
C = 6 3 - 4 3 + 2
3
6 - 4 + 2 = 2 + 2 = 4
C = 4 3
Mon calcul est terminé : je vérifie que la
consigne est respectée : écrire sous la forme
a 3 où a est un nombre entier :
4 3 est bien sous la forme a 3 et a
est bien entier a = 4 ; la consigne est respectée
Mon 1er exercice est terminé
