|
LES VOLUMES
|

|
Je prends les surfaces
créées par les différentes figures
géométriques vues précédemment,
et je leur ajoute une dimension supplémentaire (une
3è dimension) : c'est celle de la profondeur ou la
hauteur. Mes figures deviennent alors des solides, des
objets matérialisables dans l'espace, avec un
encombrement que je peux mesurer : ce sont les
volumes.
L'unité de mesure d'un
volume est le mètre cube(m3), et autres mesures de longueur au cube
(centimètre cube, pour le plus courant) : le cube
(exposant 3), rappelle :
- la multiplication de 3
grandeurs pour chacun des volumes calculés (c'est
à dire une surface ou aire par une profondeur ou
une hauteur)
- la conversion des
unités de mesure des surfaces de trois en
trois
Exemple : 1 mètre cube = 1000
décimètres cubes = 1 000 000
centimètres cubes = 0,001 décamètre
cube
Conformément au tableau de conversion ci-dessous
:

Equivalences de
volumes qu'il faut connaître :
Puisqu'un volume est
matérialisé par un objet dans l'espace, ce
volume représente un contenant, c'est à dire qu'il a la
capacité de contenir quelque chose (un liquide par
exemple). L'unité de volume est donc très
étroitement liée à l'unité de
capacité (Litre, hectolitre,décilitre ....).
Je dois donc absolument connaître l'équivalence
des volumes en capacité
J'apprends par coeur : 1 Décimètre cube = 1
Litre
Les autres unités de capacité
s'intégreront respectivement dans les cases de part
et d'autre du litre, de 1 en 1 cette fois-ci. J'apprends le
tableau des correspondances ci-dessus.
ATTENTION : comme pour le périmètre ou
l'aire d'une figure géométrique, pour
être exprimées dans une certaine unité
de volume, (exemple le centimètre cube), toutes les
mesures prises en compte dans le calcul devront être
en centimètre. Dans le cas contraire, je serais
obligée de convertir toute valeur exprimée
dans une autre unité de mesure, avant de commencer
mon calcul, conformément au tableau de conversion des
unités de longueur (voir fiche le
périmètre)
:
Les solides peuvent être
construits en temps qu'objet : je vous donnerai pour chacun
des solides existants les particularités de leur
construction. Vous pouvez d'ailleurs vous amuser à
les construire vous-même, pour voir
concrètement ce qu'ils
représentent.
Mais, ils peuvent être
aussi représentés sur le papier : c'est
d'ailleurs comme ils se présentent à moi dans
un exercice, de calcul de volume par exemple. Je devrai
utiliser alors la notion de perspective, afin d'évoquer l'espace
occupé par le solide , et qui bien entendu, ne peut
être représenté sur une surface plane:
cette perspective sera représentée à
chaque construction par des pointillés.
Je vous donne ci-dessous les différents solides (ou
objets) que je peux construire à partir des surfaces
(ou figures) géométriques, et les formules
pour calculer leurs volumes :
 Le Cube Le Cube

|
|
Pour sa
construction dans l'espace:
- 6 faces
carrées de même
surface
|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|
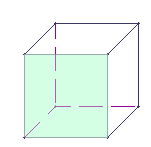
Point de
départ
: le carré :
Je trace un carré qui sera
complété par deux
parallèlogrammes dont la mesure du
côté est égale
à la mesure du côté du
carré. je mets en pointillé
les arêtes de mon cube qui ne se
voient pas.
|
|
Volume du
cube
|
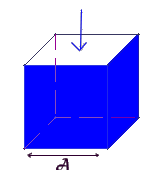
soit : Aire du carré
d'origine (A2)  profondeur du cube,
qui a la même mesure que le
côté du carré
d'origine : donc A
3 profondeur du cube,
qui a la même mesure que le
côté du carré
d'origine : donc A
3
|
Exemple sur la
figure :
si un côté du
carré d'origine mesure 4
cm, le volume du cube
correspondant sera égal
à 43 = 64
cm3
|
|
|
 Le Pavé Le Pavé

|
|
Pour sa
construction dans l'espace:
- 6 faces
rectangulaires dont les surfaces sont
les mêmes 2 à
2
|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|
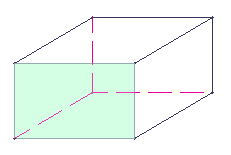
Point de départ :
le
rectangle
Je
trace un rectangle, et lui ajoute deux
parallèlogrammes de dimensions
différentes
je mets en pointillé les
arêtes de mon pavé qui ne se
voient pas.
|
|
Volume du
pavé
|

|
|
 Le Prisme Le Prisme

|
|
Pour sa
construction dans l'espace:
- 2 faces,
de même forme
géométrique et de
même surface, appelées
bases du prisme
- Autant
de faces rectangulaires qu'il y a de
côtés à la
base,
|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|

Point de départ :
un polygone à 4, 5,
6 ....
côtés.
Je trace mon polygone puis crée des
segments issus de chacun des sommets du
polygone de base : mes segments devront
tous avoir la même longueur et
être parallèles. Les
extrêmités de ces segments
ainsi crées deviendront les sommets
de mon 2è polygone, image du 1er,
et 2ème base de mon prisme : je
mets en pointillé les arêtes
de mon prisme qui ne se voient
pas.
|
|
Volume du
prisme
|
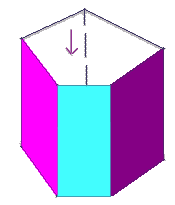
Base
 Hauteur
Hauteur
|
Base : Aire du
polygone sur lequel repose le
prisme
H = Profondeur du
prisme
|
Exemple sur la
figure :
J'ai calculé l'aire de mon
polygone de base,
conformément à la
formule de calcul correspondante
(voir fiche : les
aires)
Aire du polygone = 35
cm2
Si la profondeur ajoutée
mesure 5 cm , le volume de mon
prisme ainsi crée sera
égal à 35  5 = 175
cm3 5 = 175
cm3
|
|
|
 La Pyramide La Pyramide

|
|
Pour sa
construction dans l'espace:
- 1 face
formée par un
quadrilatère, appelée
base de la pyramide
- 4 faces
triangulaires joignant cette
base
|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|
|
 Point de départ :
un quadrilatère
Point de départ :
un quadrilatère
Après avoir
tracé mon quadrilatère, (ici
un parallèlogramme), je relie ses 4
sommets à un point du plan qui
deviendra sommet de ma pyramide : je mets
en pointillé les arêtes de ma
pyramide qui ne se voient pas.
|
|
Volume de la
pyramide
|
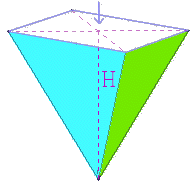
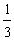 Base Base  Hauteur
Hauteur
|
Base : surface du
quadrilatère de
base
H =
hauteur de la pyramide : c'est le
segment issu du centre des
diagonales du
quadrilatère, base de la
pyramide jusqu'au sommet de la
pyramide.
|
Exemple sur la
figure :
J'ai calculé l'aire de mon
parallèlogramme de base,
conformément à la
formule de calcul correspondante
(voir fiche : les
aires).
Aire = 12 cm2
Si j'ajoute une hauteur de 8 cm,
ma pyramide ainsi
créée aura un
volume de :
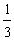  12 12  8 = 32
cm3 8 = 32
cm3
|
|
|
 Le Cylindre Le Cylindre

|
|
Pour sa
construction dans l'espace:
- 2 faces
rondes (ou ovales), de même
surface, appelées bases du
cylindre
- 1 "face"
rectangulaire qui permettra d'effectuer
"l'enroulement" du
cylindre
|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|
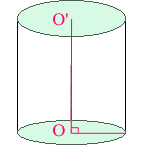
Point de départ :
le cercle (ou
l'ellipse)
Je construis 1premier cercle (ou
elllipse). Je trace un segment OO'
perpendiculaire au rayon du cercle : O'
deviendra le centre de mon deuxième
cercle (ou elllipse). je relie les
extrêmités des 2 cercles
entre elles : j'obtiens mon
cylindre.
|
|
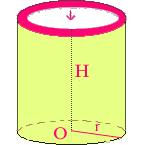
Volume du
cylindre
|
|
Base correspond
à
l'aire du
disque, base du
cylindre
H est la hauteur du cylindre :
segment qui relie les 2 centres
des disques de base
|
Exemple sur la
figure :
J'ai calculé l'aire du
disque, base du cylindre,
conformément à la
formule de calcul correspondante
(voir fiche : les
aires).
Aire = 12 cm2
Si j'ajoute une hauteur de 5 cm,
mon cylindre ainsi crée
aura un volume de :
12  5 = 60
cm3 5 = 60
cm3
|
|
|
 Le Cône Le Cône
(de révolution)

|
|
Pour sa
construction dans l'espace:
- 1 face
ronde (ou ovale), appelée base
du cône
- 1 "face"
triangulairre qui permettra d'effectuer
"l'enroulement" du
cône
|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|

Point de départ :
le cercle (ou
l'ellipse)
Je construis un cercle (ou ellipse). Je
prends les extrêmités du
cercle ainsi tracé, et les relie
entre elles : leur intersection forme le
sommet de mon cône
|
|
Volume du
cône
|

|
Base correspond
à
l'aire du
disque, base du
cylindre
H est la hauteur du cylindre :
segment qui relie les 2 centres
des disques de base
|
Exemple sur la
figure :
J'ai calculé l'aire du
disque, base du cône,
conformément à la
formule de calcul correspondante
(voir fiche : les
aires).
Aire = 12 cm2
Si j'ajoute une hauteur de 5 cm,
mon cône ainsi crée
aura un volume de :
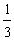  12 12  5 = 20
cm3 5 = 20
cm3
|
|
|
 La sphère La sphère
(boule)

|
|
|
Représentation sur
le papier :
|

|
|
Construction
:
|
|
 Point de départ :
le
cercle
Point de départ :
le
cercle
Je trace un cercle: l'épaisseur de
ma sphère sera
matérialisée par des
pointillés (car elle n'est pas
visible dans un plan) : les
pointillés forment un ron ellipse,
de centre O, centre du cercle, et ayant
les mêmes extrêmités
que le cercle d'origine.
|
|
Volume de la
sphère
|

|
|
|

