LES TRIANGLES

Caractéristiques des triangles

Comme son nom l'indique, un triangle est une figure à "3'" : tri = trois
trois côtés
trois angles
trois sommets : sommet : points, extrêmités des 3 segments qui forment le triangle :

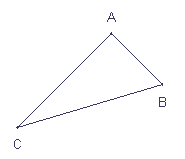
les points A B C sont les 3 sommets du triangle AB- BC et CA sont les 3 côtés CAB - ABC et BCA sont les 3 angles Règle : la somme des 3 angles d'un triangle est toujours égale à 180° Base du triangle : on appelle base d'un triangle, le côté sur lequel "il se pose. Le sommet opposé à cette base s'appelle le sommet principal du triangle. La base du triangle peut être indifféremment l'un des 3 côtés. ex : si je prends pour base de mon triangle le côté CB, A sera le sommet principal de mon triangle.

Tel se caractérise un triangle. Il existe maintenant des triangles particuliers, de par leurs côtés et ou leurs angles ; étudions les :

Le triangle isocèle

Caractéristiques :
Triangle dont 2 des côtés et des angles sont égaux (de même mesure)
Construction :
Je trace un premier segment (base du triangle), puis avec un compas je prends un écartement équivalent à la mesure de mes 2 côtés égaux : à la 1ère extrémité de la base, un petit trait de compas équivalent à l'écartement - même chose à la 2è extrémité, et voilà j'obtiens le sommet de mon triangle

Propriétés :

Issues de ses caractéristiques : Si un triangle est isocèle, alors il a 2 côtés égaux - et la propriété inverse : si un triangle a deux côtés égaux, alors il est isocèle. La base d'un triangle isocèle est le côté dont la mesure est différente des 2 autres sur le dessin : base = CB Dans un triangle isocèle, les 2 angles de la base sont de même mesure- et la propriété inverse : si un triangle a les 2 angles de sa base de même mesure, alors il est isocèle. Si dans un triangle, deux des éléments parmi hauteurs, médianes, médiatrices, bissectrices sont confondus, alors ce triangle est isocèle. (voir droites particulières ci-dessous).

 

 

Le triangle équilatéral

Caractéristiques :
Triangle dont les 3 côtés et les 3 angles sont égaux (de même mesure) - Mesure d'un angle = 60°
Construction :
Même chose que pour le triangle isocèle sauf que l'écartement de mon compas sera équivalent à la mesure de la base, puisque mes 3 côtés doivent être égaux

Propriétés :

Issues de ses caractéristiques : Si un triangle est équilatéral, alors ses 3 côtés sont égaux - et la propriété inverse : si un triangle a ses 3 côtés égaux, alors il est équilatéral Un triangle équilatéral a ses 3 angles de même mesure = 60°- et la propriété inverse : si un triangle a ses 3 angles de même mesure = 60°, alors il est équilatéral Propriétés annexes : Si un triangle a deux angles de 60°, alors c'est un triangle équilatéral. logique que le3è angle mesure aussi 60°, car sur un total de 180° (somme des 3 angles d'un triangle) 180° - 120° (2 60) = 60° non ?? Si un triangle isocèle a un angle de 60°, alors il est équilatéral. Toujours aussi logique, car on a vu plus haut qu'un triangle isocèle a deux angles égaux : donc toujours sur un total de 180°: 180° - 60°= 120 ° et 120° / 2 (car réparti sur les 2 angles égaux) = 60°. Magique non ???

 

 

Le triangle rectangle

Caractéristiques :
Triangle dont 2 des côtés sont perpendiculaires (forment un angle droit : 90°) Vocabulaire : Hypoténuse : l'hypoténuse est particulière au triangle rectangle : on appelle hypoténuse le côté du triangle qui est opposé (en face de) à l'angle droit. Ex: dans le triangle ABC, BC = hypoténuse
Construction :
Je construis les 2 côtés de l'angle droit avec mon équerre. Je relie ensuite ces 2 côtés entre eux pour obtenir mon 3è côté.

Propriétés :

Issues de ses caractéristiques : Si un triangle est rectangle, alors un de ses angles est un angle droit, et 2 de ses côtés sont perpendiculaires Exemple : dire que le triangle ABC est rectangle en A, c'est dire que A est un angle droit (mesure = 90°) et que (AC) et (AB) sont perpendiculaires et la propriété inverse : Si 2 des côtés d'un triangle sont perpendiculaires, alors le triangle possède un angle droit : il est rectangle. Si un triangle possède 2 angles complémentaires, alors il est rectangle. Rappel : angles complémentaires : angles dont la somme de leurs mesures est égale à 90° (angle droit) (voir fiche). Si vous avez compris les angles, il n'y a rien de plus logique : on sait que la somme des 3 angles d'un triangle doit toujours être égale à 180° : si deux de mes angles sont complémentaires, ils mesurent à eux 2 90°. Il est donc logique que le 3è angle mesure 90° et donc soit droit : 180° - 90° = 90° . Voilà pourquoi il est normal que, à cette condition, le triangle soit rectangle !! Le triangle rectangle est l'hôte du théorème de Pythagore et des formules trigonométriques (voir fiches respectives) Enfin, il existe une propriété commune à tous les types de triangles, puisque non issue des caractéristiques de chacun d'entre eux, c'est le théorème des milieux : Dans un triangle, si une droite passe par le milieu de 2 des côtés, alors elle est parallèle au 3è côté et la propriété inverse (réciproque du théorème des milieux) : dans un triangle, si une droite passe par le milieu d’un côté et est parallèle à un deuxième côté,. alors elle passe par le milieu du troisième côté

Les droites particulières du triangle

Il existe plusieurs catégories de droites particulières au triangle:

Les hauteurs

Une hauteur est une droite qui passe par un des sommets et est perpendiculaire au côté opposé à ce sommet Tracé des 3 hauteurs : je pars d'un des sommets et avec mon équerre trace une droite perpendiculaire au côté opposé au sommet

Propriétés :

Les 3 hauteurs du triangle se coupent en un même point appelé orthocentre du triangle. Point O sur le dessin Si une droite est hauteur dans un triangle, alors elle est perpendiculaire à un côté et passe par le sommet opposé. et la propriété inverse : Si une droite est perpendiculaire à un des côtés d'un triangle et passe par son sommet opposé, alors cette droite est l'une des 3 hauteurs du triangle. Particularité du triangle isocèle : Dans un triangle isocèle, la hauteur issue de l'angle principal est aussi bissectrice de l'angle, médiane et médiatrice du côté opposé (base). Cela signifie que la hauteur issue de l'angle principal coupe cet angle en 2 angles égaux (bissectrice) et passe par le milieu de la base (médianes et médiatrices). Voir + bas

Les médianes

Une médiane est une droite qui passe par un des sommets et par le milieu du côté opposé à ce sommet. Tracé des 3 médianes : je prends les milieux de chacun des 3 côtés et les relient au sommet du triangle qui leur est opposé

Propriétés :

Les 3 médianes d'un triangle se coupent en un même point appelé centre de gravité du triangle ce centre de gravité se situe aux 2/3 de chaque médiane en partant du sommet. Dans un triangle, si une droite est médiane, alors elle passe par le milieu d'un côté etpar le sommet opposé et la propriété inverse : dans un triangle, si une droite passe par le milieu d'un côté et par le sommet opposé, alors cette droite est une médiane du triangle Particularité du triangle rectangle : Dans un triangle rectangle, la longueur de la médiane issue de l'angle droit est égale à la moitié de la longueur l'hypoténuse. Exemple :Soit ABC un triangle rectangle en A. La médiane de l'angle  passera donc par le milieu du segment BC, hypothénuse. On nommera ce point le point O On peut donc écrire : 0B = OC = OA Ce qui implique la propriété suivante : Dans un triangle rectangle, le milieu de l'hypothénuse est équidistant des 3 sommets du triangle. D'où la formation de 2 triangles isocèles AOB et AOC et la propriété inverse : Si dans un triangle, la longueur de la médiane relative à un côté est égale à la moitié de la longueur de ce côté, alors ce triangle est rectangle. Particularité du triangle isocèle : Dans un triangle isocèle, la médiane issue de l'angle principal est aussi bissectrice de l'angle, hauteur et médiatrice du côté opposé (base). Cela signifie que la médiane issue de l'angle principal coupe cet angle en 2 angles égaux (bissectrice) et est perpendiculaire à la base (médiatrices et hauteurs).

Les médiatrices

Comme pour n'importe quel segment (voir fiche), c'est une droite qui passe par le milieu d'un des côtés du triangle et qui est perpendiculaire à ce même côté. Tracé des 3 médiatrices : je prends les milieux de chacun des 3 côtés et trace avec mon équerre la perpendiculaire passant par ce milieu.je peux aussi construire les médiatrices avec mon compas (explication sur la fiche "la médiatrice d'un segment : voir fiche)

Propriétés :

Les 3 médiatrices d'un triangle se coupent en un même point qui est le centre du cercle circonscrit au triangle. Qu'est-ce qu'un cercle circonscrit à un triangle ? C'est un cercle qui passe par les 3 sommets du triangle. Dans un triangle, si une droite est médiatrice, alors elle passe par le milieu d'un côté et est perpendicualaire à ce côté et la propriété inverse : dans un triangle, si une droite passe par le milieu d'un côté et est perpendiculaire à ce côté, alors cette droite est une médiatrice du triangle : je peux alors appliquer les mêmes propriétés que pour la médiatrice d'un segment (voir fiche) Particularité du triangle rectangle : Dans un triangle rectangle, le centre du cercle circonscrit (point de rencontre des 3 médiatrices) est le milieu de l'hypoténuse. et la propriété inverse : dans un triangle, si le centre du cercle circonscrit est le milieu de l'hypoténuse (c'est à dire le côté opposé à l'angle qu'on pense être droit), alors le triangle est effectivement un triangle rectangle. Particularité du triangle isocèle : Dans un triangle isocèle, la médiatrice de la base est aussi bissectrice de l'angle principal, hauteur issue de cet angle et médiane de la base . Cela signifie que la médiatrice de la base passe par le sommet principal (hauteur et médianes) et coupe l'angle principal en 2 angles égaux (bissectrice).

Les bissectrices

Comme je l'ai déjà vu dans la fiche sur les angles, une bissectrice est une droite qui coupe un angle en 2 angles égaux. Dans un triangle, c'est donc la droite qui coupe un angle du triangle en deux angles égaux. Tracé des 3 bissectrices : Rappel de l'explication donnée dans la fiche les angles Avec un compas : je pose la pointe de mon compas sur un des sommets du triangle. je prend un petit écartement et je marque chacun des 2 côtés de mon sommet avec cet écartement. Je place la pointe de mon compas successivement sur chacune des marques des côtés, et avec un plus grand écartement, vais marquer leur point de rencontre. La bissectrice passera par le sommet concerné et le point ainsi tracé.

Propriétés :

Les 3 bissectrices d'un triangle se coupent en un même point qui est centre du cercle inscrit dans le triangle. Si dans un triangle,une droite est la bissectrice d'un des 3 angles, alors elle coupe cet angle en 2 angles égaux et la propriété inverse : si dans un triangle, une droite coupe un des 3 angles en 2 angles égaux, alors cette droite est la bissectrice de cet angle: je pourrai donc utliser les mêmes propriétés déjà vues dans la fiche les angles "Bissectrice d'un angle" (voir fiche) Particularité du triangle isocèle : Dans un triangle isocèle, la bissectrice de l'angle principale est aussi hauteur issue de cet angle, médiatrice et médiane de la base .Cela signifie que la bissectrice de l'angle principal passe par le milieu de la base (médiane et médiatrice) et est perpendiculaire à cette base (médiatrice et hauteur).