LES QUADRILATERES

Caractéristiques des quadrilatères

Comme son nom l'indique, un quadrilatère est une figure à "4'" : quadra = quatre

Quatre côtés
Quatre angles
Quatre sommets : sommet : points,extrêmités des 4 segments qui forment le quadrilatère : je peux relier 2 à 2 les sommets opposés du quadrilatère : les segments ainsi formés s'appellent les diagonales du quadrilatère : elles se coupent entre elles. Ce sont les seules droites particulières aux quadrilatères

les points A B C et D sont les 4 sommets du quadrilatère AB- BC- CD et DA sont les 4 côtés DAB - ABC - BCD et CDA sont les 4 angles AC et DB sont les 2 diagonales du quadrilatère

Ce sont les caractériqtiques d'un quadrilatère.Il existe des quadrilatères particuliers, dont les côtés, les angles et/ou les diagonales répondent à des exigences particulières. Etudions les :

Le trapèze

Caractéristiques :
2 des côtés du trapèze sont parallèles Les diagonales du trapèze ne se coupent pas en leur milieu
Construction :
Je trace un 1er segment : je trace un 2è segment parallèle au 1er : je relie les 4 points des 2 segments 2 à 2

Propriétés :

Issues de ses caractéristiques : Si un quadrilatère est un trapèze, alors ses deux bases sont parallèles. et la propriété inverse : si un quadrilatère a ses 2 bases parallèles, alors c'est un trapèze Particularités: un trapèze peut être un trapèze rectangle : dans ce cas il aura 2 angles droits Un trapèze peut aussi être un trapèze isocèle : dans ce cas deux de ses côtés (qui ne sont pas les bases), sont de même longueur.

 

 

Le parallèlogramme

Caractéristiques :
Ses côtés sont parallèles 2 à 2 Ses côtés sont de même mesure 2 à 2 Ses diagonales se coupent en leur milieu mais ne sont pas de même mesure
Construction :
Je trace un 1er segment : je trace une droite parallèle à ce segment : je prend une des extrêmités du segment et la relie à un point de la droite. Par la 2è extrémité du segment je trace la parallèle au nouveau segment que je viens de tracer. l'intersection de cette parallèle et de ma 1ère droite, sera le 4è sommet de mon parallèlogramme. OU Je trace ses diagonales : 2 segments de mesure différente : leurs 2 milieux deviennent leur point d'intersection: il ne me reste plus qu'à joindre les extrêmités des segments 2 à 2

Propriétés :

Issues de ses caractéristiques : Si un quadrilatère est un parallélogramme (losange, rectangle, carré), alors ses côtés opposés sont parallèles deux à deux. Si un quadrilatère est un parallélogramme alors ses côtés opposés sont parallèles deux à deux. Si un quadrilatère est un parallélogramme, alors ses angles opposés ont, deux à deux, la même mesure Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont deux à deux de même longueur. Si un quadrilatère est un parallèlogramme, alors ses diagonales ont le même milieu  Si ABCD est un parallèlogramme, alors = voir les fiches : Création d'image Calculs dans un repère pour une explication détaillée des vecteurs    Et les propriétés inverses

  

Le rectangle

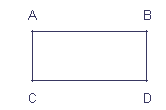
Caractéristiques :
Ses côtés sont parallèles 2 à 2 ; Ses côtés sont de même mesure 2 à 2 Ses côtés consécutifs sont perpendiculaires 2 à 2 Ses diagonales se coupent en leur milieu et sont de même mesure
Construction :
Soit : Je construis le rectangle par ses diagonales : au compas : je plante la pointe de mon compas en un point qui sera le centre de mes diagonales : je choisi un écartement et trace quatre marques de part et d'autres du centre des diagonales. J'obtiens ainsi les 4 sommets de mon rectangle : je peux les relier consécutivement, 2 à 2   Soit : Je trace les côtés du rectangle : je commence par tracer 2 segments de longueur différente, mais perpendiculaires ; j'utilise pour cela mon équerre. J'obtiens ainsi 3 des sommets de mon rectangle. Pour tracer le 4è sommet, j'utilise le compas : je prends l'écartement de mon premier segment et le reporte à l'extrêmité du 2è segment ; je prends l'écartement du 2è segment, et le reporte à l'extrênité du 1er ; le point ainsi tracé sera le 4è sommet de mon rectangle ; je le relie 2 à 2 avec les points consécutifs.

Propriétés :

Issues de ses caractéristiques : Si un quadrilatère a trois angles droits, alors c'est un rectangle. Si un parallélogramme a un angle droit, alors c'est un rectangle. Si un parallélogramme a ses diagonales de même longueur, alors c'est un rectangle. Si un quadrilatère est un rectangle alors ses côtés opposés sont parallèles deux à deux.  Si un quadrilatère est un rectangle (carré), alors ses côtés consécutifs sont perpendiculaires deux à deux. Le rectangle est un parallèlogramme particulier : il possède donc les mêmes propriétés que ce dernier. (voir ci-dessus) Et les propriétés inverses

Le losange

Caractéristiques :
Ses côtés sont parallèles 2 à 2 ; Ses 4 côtés sont de même mesure Ses diagonales se coupent en leur milieu mais ne sont pas de même mesure Elles sont perpendiculaires
Construction :
Construction par ses diagonales : Je trace 2 segments perpendiculaires, de mesure différente: leurs 2 milieux deviennent leur point d'intersection: il ne me reste plus qu'à joindre les extrêmités des segments 2 à 2 :j'ai mon losange

Propriétés :

Issues de ses caractéristiques : Si un quadrilatère est un losange (carré), alors ses diagonales sont perpendiculaires. Si un quadrilatère est un losange (carré), alors ses 4 côtés ont la même longueur.   Si un quadrilatère a quatre côtés de même longueur, alors c'est un losange.  Si un parallélogramme a deux côtés consécutifs de même longueur, alors c'est un losange.  Si un parallélogramme a ses diagonales perpendiculaires, alors c'est un losange. Dans un losange les diagonales sont les bissectrices des angles.: cela signifie que pour montrer par exemple que l'angle de sommet B est coupé en 2 angles égaux, il me suffit de montrer que la figure concernée est un losange(peut-être me le dira-t-on ou puis-je le montrer en utilisant les propriétés de ses caractéristiques), et que la droite qui passe par le sommet B est la diagonale du losange DONC bissectrice DONC coupe l'angle de sommet B en 2 (la bissectrice d'un angle coupe un angle en 2 : voir fiche les angles)   Et les propriétés inverses

Le carré

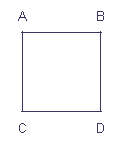
Caractéristiques :
C'est le quadrilatère le + particulier : c'est un mélange du rectangle et du losange Ses côtés sont parallèles 2 à 2 ; Ses 4 côtés sont de même mesure Ses diagonales se coupent en leur milieu et sont de même mesure Elles sont perpendiculaires
Construction :
Soit : Je construis le carré par ses diagonales : comme pour le losange, je trace deux segments perpendiculaires : le point d'intersection de ces segments devient le centre de mes diagonales. 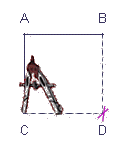Comme pour le rectangle, et pour que mes diagonales soient de même mesure, je vais utiliser le compas : je plante la pointe de mon compas en ce point centre de mes diagonales : je choisi un écartement et trace quatre marques de part et d'autres des 2 segments : J'obtiens ainsi les 4 sommets de mon carré : je peux les relier consécutivement, 2 à 2 Soit : Je trace les côtés du carré : je commence par tracer 2 segments perpendiculaires de même longueur : j'utilise pour cela mon équerre. J'obtiens ainsi 3 des sommets de mon carré. Pour tracer le 4è sommet, j'utilise le compas : je prends l'écartement d'un de mes 2 segments (puisque le même) et le reporte à l'extrêmité du 2è segment ; puis du 1er segment. le point ainsi tracé sera le 4è sommet de mon carré ; je le relie 2 à 2 avec les points consécutifs.

Propriétés :

Issues de ses caractéristiques : Si un rectangle a deux côtés consécutifs de même longueur, alors c'est un carré. Si un quadrilatère est à la fois un losange et un rectangle, alors c'est un carré. Si un losange a ses diagonales de même longueur, alors c'est un carré. Si un rectangle a ses diagonales perpendiculaires, alors c'est un carré. Si un losange a un angle droit, alors c'est un carré.   Et les propriétés inverses