|
|
CREATION D'IMAGES
|
|
Cette fiche traite des
différentes transformations que peuvent subir un
point, un segment ou une figure géométrique
:
C'est créer
l'image d'un point, segment ou figure par rapport à
un centre de symétrie (point)
|
Caractéristiques
:
|
|
|
Créer l'image d'un point par une
symétrie centrale, c'est construire un
segment, passant par le centre de symétrie,
et avec le centre de symétrie pour
milieu
Exemple d'énoncé : construire A' l'image de A par
la symétrie de centre O
Le support pour la
création de mon image est un point : je suis
en symétrie centrale : je trace donc le
segment AA' passant par O, avec O milieu du segment
AA'
|
|
|
Construction
:
|
|
|
Je trace les demi-droites passant par le centre de
symétrie O, issues respectivement de A, B et
C
Avec mon compas : je place la pointe de mon conmpas
en O : je prend la mesure AO - BO et CO et les
reporte sur la 2è portion des 3 droites :
les marques ainsi tracées
représentent mes points A',B' et C'
symétriques de A, B et C par rapport
à O.
|
|
Propriétés :
|
Issues de ses caractéristiques
:
 Si A' image de A par la
symétrie de centre O, alors O est le milieu
du segment AA'. Je peux alors appliquer les
mêmes propriétés que pour le
milieu d'un segment
L'image d'une droite par une
symétrie centrale, est une droite
parallèle.
Propriété
générale des transformations
:
La symétrie centrale, comme la
symétrie axiale, la rotation et la
translation conserve :
les mileux
le parallélisme
les angles (donc l'orthogonalité)
les distances
l'alignement
(voir
propriétés communes ci-dessous)
|
C'est créer
l'image d'un point, segment ou figure par rapport à
un axe (droite)
Aussi appelée
réflexion
|
Caractéristiques
:
|
|
|
Créer l'image d'un point par une
symétrie axiale, c'est construire un
segment, avec l'axe de symétrie
médiatrice de ce
segment
Rappel
: la
médiatrice d'un segment est la droite qui
passe par le
milieu
de ce segment et est perpendiculaire à ce segment
Exemple d'énoncé : construire A' symétrique
de A par rapport à la droite
(D)
Le support pour la
création de mon image est une droite : je
suis en symétrie axiale : je trace donc le
segment AA' perpendiculaire à la droite (D)
avec (D) passant par le milieu de AA' (d'où
(D) médiatrice de AA')
|
|
|
Construction
:
|
|
|
Avec mon équerre, je trace 3 demi-droite
perpendiculaires à (D) issues respectivement
de A,B et C. Avec mon compas : Je plante la pointe
de mon compas sur la droite (D) et mesure les
distances avec chacun des points : je reporte
chacun des écartements sur les demi-droites
correspondantes : les marques ainsi
créées représentent mes points
A',B' et C' symétriques de A, B et C par
rapport à l'axe (D)
|
|
Propriétés :
|
Issues de ses caractéristiques
:
Si A' symétrique de A par
rapport à (D), alors la droite (D) est la
médiatrice du segment AA'. Je peux alors
appliquer les mêmes propriétés
que pour la médiatrice d'un segment
Propriété
générale des transformations
:
La symétrie axiale, comme la
symétrie axiale, la rotation et la
translation conserve :
les mileux
le parallélisme
les angles (donc l'orthogonalité)
les distances
l'alignement
(voir
propriétés communes ci-dessous)
|
C'est créer
l'image d'un point, segment ou figure par rapport à
un centre de rotation (point) et à un angle
|
Caractéristiques
:
|
|
|
Créer l'image d'un point par une rotation,
c'est construire un angle qui aura pour
sommet
le centre de la rotation, pour mesure le degrés de la
rotation et 2 côtés
égaux
Exemple
d'énoncé : construire A' image de A par la
rotation de centre O et d'angle
60°
Les supports pour la
création de mon image sont un point et un
angle : je suis en rotation : je place donc le
point A' tel que mon angle AOA' (sommet O) soit
égal à 60° et que AO =
OA'
|
|
|
Construction
:
|
|
|
Je trace les demi-droites passant par O issues de A
et B
Je place le point 0
de mon rapporteur sur le point O et le fait pivoter
sur cet axe, pour le "poser" sur le
côté que je viens de tracer. A la
graduation 60 du rapporteur, je fais une marque :
cette marque sera un point de mon 2è
côté de l'angle : je peux donc
maintenant tracer une 2è demi-droite issue
de O et passant par ce point ainsi
tracé.
Le point B' image de B par la rotation se trouve
quelque part sur cette 2è demi-droite.
Pour connaître la distance de OB' je prends
mon compas : Je plante la pointe de mon compas en O
et mesure la distance à B : je reporte
l'écartements sur ma nouvelle demi-droite :
la marque ainsi créée
représente le point B' image de B par la
rotation de centre O et d'angle
60°
Sens de la
rotation :
On peut m'indiquer un sens pour la rotation : Soit
:
Le sens des aiguilles d'une montre ou rotation
horaire: (de haut en bas) A' se situera donc + bas
que le sommet O de l'angle
Le sens inverse des aiguilles d'une montre (ou
rotation anti-horaire) (de bas en haut) A' se
situera donc + haut que le sommet O de l'angle
La rotation réalisée sur la figure
d'exemple est une rotation horaire
|
|
Propriétés :
|
Issues de ses caractéristiques
:
Par la rotation, je crée un
angle dont la mesure est égale à
l'angle de la rotation (ex : rotation d'angle
60°  la mesure de mon
angle AOA' est égale à 60°)
Par la rotation, je crée un
angle dont les côtés sont de
même mesure
Propriété
générale des transformations
:
La rotation comme les symétries
et la translation conserve :
les mileux
le parallélisme
les angles (donc l'orthogonalité)
les distances
l'alignement
(voir
propriétés communes ci-dessous)
|
C'est créer
l'image d'un point, segment ou figure par rapport à
deux points ou vecteur
|
Caractéristiques
:
|
|
|
Créer l'image d'un point par une
translation, c'est construire un vecteur,
égal au vecteur de
référence
Rappel
1: qu'est-ce qu'un
vecteur ?
Notation : exemple : vecteur EF noté 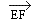 Un vecteur possède
:
- une direction
(c'est la pente du segment représentant
le vecteur)
- un sens (ex :
sens de 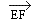= de E vers
F)
- une longueur (ex
: longeur de 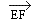= distance
EF)
Rappel
1:
égalité de vecteurs
Règle : 2 vecteurs sont égaux
s'ils ont le même sens, la même
direction et la même longueur
Important : dire que 2 vecteurs sont égaux
revient à dire que les segments
formés par ces 2 vecteurs
sont
parallèles (cf définition du
parallélisme dans fiche sur droites &
segments)
Exemple
d'énoncé : construire A' image de A par la
translation de vecteur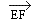
On peut trouver aussi : construire A' image de A
par la translation qui transforme E en F
Le support pour la création de mon image est
un vecteur (ou 2 points) : je suis en translation :
je vais donc construire A' pour que  =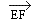
|
|
|
Construction
:
|
|
|
Exemple : construction de AA'
Je vais donc construire A' pour que =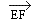
Conformément à la règle
d'égalité de 2 vecteurs :
doit avoir le même sens
que 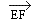: je pars de la gauche pour aller
vers la droite
doit avoir la même direction
que 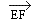: je trace donc la parallèle
à (EF) en A
doit avoir la même mesure que
:
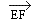avec mon compas, je prends la mesure de EF et la
reporte en A : la marque ainsi tracée
devient A' :
les critères d'égalité de 2
vecteurs sont respectés A' est bien l'image
(on dit aussi le translaté) du point A par
la translation de vecteur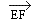
|
|
|
Les propritétés
générales des
transformations
|
Ces
propriétés sont très importantes, et
sont valables pour toutes les transformations que je viens
de voir :
|
Les transforamtions conservent les
milieux
|
Aussi, si M mileu de AB alors
M' image de M par la symétrie de centre O, d'axe D,
la rotation d'angle  ou de
translation de vecteur  sera
le milieu de A'B' image du segment AB par cette
symétrie centrale, cette symétrie axiale,
cette rotation ou cette translation
|
Les transforamtions conservent le
parallèlisme
|
Aussi, si deux 2 droites (A)
et (B) sont parallèles, alors (A') et (B') images de
ces droites par la symétrie de centre O, d'axe D, la
rotation d'angle ou de translation de vecteur
seront parallèles
|
Les transforamtions conservent les
angles
|
1) Aussi, si l'angle  mesure
60°, alors  image de cet angle par la symétrie de
centre O, d'axe D, la rotation d'angle ou de
translation de vecteur
mesurera 60°
2) Aussi, si les droites (D) et (F) sont perpendiculaires
(forment un angle de 90°), alors (D') et (F'), images
de ces droites par la symétrie de centre O, d'axe D,
la rotation d'angle ou de
translation de vecteur
seront deux droites perpendiculaires.
|
Les transforamtions conservent les
distances
|
Aussi, si un segment AB mesure
3 cm, A'B' image de ce segment par la symétrie de
centre O, d'axe D, la rotation d'angle ou
de translation de vecteur
mesurera 3 cm
|
Les transforamtions conservent
l'alignement
|
Aussi, si 3 points A, B et
C sont alignés, alors A', B' et C' image de ces
points par la symétrie de centre O, d'axe D, la
rotation d'angle ou
de translation de vecteur
seront alignés
Et voilà ! Elles sont bien ces transformations non
?? Les propriétés des transformations,
qu'elles soient particulières à chacune
d'elles ou générales sont très
utiles, notamment pour les démonstrations.
On peut me donner par exemple à tracer un point
O', symétrique d'un point A par un point O. On me
demandera ensuite de démontrer que O est le milieu
de AA'. Pour cela, je dois savoir que en symétrie
centrale, mon point centre de symétrie devient
milieu du segment formé par mon point de
départ et son image. Vous voyez que c'est bien
utile !!
ATTENTION :
|
Cas particulier de
transformations successives
|
Cas particuliers des
transformations successives
Je dois également savoir (car cela peut me servir,
bien évidemment) que :
|
2 symétries centrales
successives = 1 translation
|
C'est celle qui transforme
un point d'origine en un point du résultat de la
2è symétrie.On dit aussi que c'est une
translation de vecteur égal à 2 fois  ,vecteur formé par les 2 centres de
symétrie
|
2 symétries axiales
successives = 1 symétrie
centrale
|
La figure jaune est l'image
de la figure bleue par ma 1erè symétrie,
d'axe vertical ; la figure rose est l'image de ma figure
jaune par ma 2è symétrie, d'axe horizontal
: Résultat : la figure rose est l'image de la
figure bleue par une symétrie de centre O
|
2 symétries axiales
successives = 1 translation
|
La figure jaune
est l'image de la figure bleue par ma 1erè
symétrie d'axe vertical ; la figure rose est l'image
de ma figure jaune par ma 2è symétrie d'axe
vertical : Résultat : la figure rose est l'image de
la figure bleue par la translation qui transforme un point
de la figure bleue en son image sur la figure
rose
|
2 translations successives = 1
somme de 2 vecteurs
|
Cette
propriété de 2 translations successives est
très importantes,car c'est le prncipe même de
la relation vectorielle de Chasles :
Interprétation :
Je pars de A pour arriver en B - Puis, je pars de B pour
arriver en C = Résultat : cela équivaut
à partir de A pour arriver en C - DONC :  +  =  (le point B commun, extrêmité de
vecteur puis origine s'annule) : C'est ça, la
relation de Chasles !!
A quoi va me
servir cette relation ?
|
:
Résultat : la figure rose est l'image de la figure
bleue par la translation de vecteur 
.
+
, d'après la
relation de Chasles
, d'après la relation de Chasles