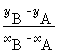|
|
LES FONCTIONS (suite)
|
|
<< Précédent
|
fonctions et représentation
graphique
|
Réfléchissons : comment utiliser une fonction
dans un graphique ??
Et bien c'est très simple : imaginez par exemple
l'exercice suivant :
Soit la fonction f(x) = 4 +2 pour reprendre notre
exemple :
Compléter le tableau suivant, avec les images de la
fonction :
Et représentez ce tableau dans un graphique :
On utilisera l'axe des abscisses pour les valeurs de x
Et l'axe des ordonnées, pour la valeur des images
Alors ?? Comment allons-nous procéder ??
1/ Pour compléter le tableau :
Nous avons déjà calculé toutes ces
images de la fonction, ci-dessus : il n'est donc pas
difficile de compléter le tableau :
|
f(3)
|
f(4)
|
f(10)
|
f(8)
|
|
14
|
18
|
42
|
34
|
2/ Pour représenter ce tableau dans un
graphique :
J'utilise la légende qu'on me propose et construis le
graphique :
 
Et maintenant : comment
placer, conformément à cette
légende, les valeurs du tableau ??
Et bien, je sais, pour avoir compris le fonctionnement du
calcul d'une fonction, que lorsque je fais :
f(3) : je remplace x par 3 dans la
fonction et son image est ainsi 14
f(4) : je remplace x par 4 dans la
fonction et son image est ainsi 18
etc....
Je peux donc dire :
pour une valeur de x = 3 ; image =
14
pour une valeur de x = 4 ; image =
18
etc....
J'obtiens ainsi ma relation valeur de x
/valeur des images :et peux alors complèter
mon graphique :
Pour la valeur des images, je prendrai comme unité
= 1 carreau = 10 unités, sinon mon graphique sera
beaucoup trop grand :
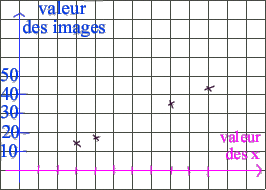
Et voilà : mes points sont tracés
conformément à ma relation valeur de x/image correspondante par ma
fonction
Je relie tous les points ainsi obtenus grâce
à la fonction f(x) :
Ces points forment une
droite (attention cependant au manque
de précision dû à l'échelle :
l'idéal de la précision est de
réaliser le graphique sur du papier
millimétré, qui donne les interlignes)
Je viens ainsi et sans le savoir, de réaliser ma
1ère représentation graphique de
fonction
Alors vos impressions ??
Concrètement cela veut dire quoi ??
Je résume ce que je viens de faire :
 Que la représentation
graphique d'une fonction est une
droite obtenue par un ensemble de
points
Et comment sont définis ces points
??
Et bien, ils sont obtenus pas la relation :
valeur de x : image correspondante
par la fonction
Je dois alors et pour cela prendre des valeurs de x, et calculer leur image par la
fonction
Ensuite, et seulement après ce calcul, je pourrai
placer cette relation dans mon graphique
Règle : les valeurs de x seront toujours
représentées sur l'axe des abscisses, les
valeurs des images obtenues par la fonction pour un x donné, seront toujours
représentées sur l'axe des
ordonnées
Bon, je trouve que j'ai bien avancé
dans mon raisonnement, et je commence à comprendre
la relation fonction/représentation graphique : je
vais maintenant essayer de résoudre le
problème suivant :
Exercice : Soit f(x) la fonction
définie par : 3x - 1
Vous représenterez graphiquement cette
fonction
Je réfléchis :
Je me souviens de ce que je viens de faire
:
"la représentation graphique
d'une fonction est une
droite obtenue par un ensemble de
points"
Les points ont été obtenus
par le calcul des images de x par
la fonction
Pour f(x) 3x - 1, je devrai
donc également calculer des images : lesquelles ??
Et bien, puisque l'on ne m'impose rien, je
pourrai calculer les images de mon
choix, génial non ??
Par exemple :
f(0) : 3
x 0 - 1 = - 1
f(1) : 3 x 1 -
1 = 3 - 1 = 2
f(2) : 3 x 2
- 1 = 6 - 1 = 5
etc....
Je peux mettre les résultats dans un tableau, pour
que ce soit plus clair pour ma représentation
graphique :
Et ainsi et comme tout à l'heure, tracer la
représentation de cette fonction dans un
repère en prenant :
- l'axe des abscisses pour les valeurs de x
- l'axe des ordonnées pour les images de
x correspondantes par la
fonction :
Comme tout à l'heure également, je
prépare mes associations :
pour une valeur de x = 0 ; image =
(-1)
pour une valeur de x = 1; image =
2
pour une valeur de x = 2; image =
5 etc....
Je peux alors tracer mes points, conformément
à la légende du repère :
Je prends cette fois-ci comme échelle :
sur x et sur y 1
graduation = 1 unité
Une fois que les 3 points que j'ai calculés sont
placés, je peux les relier entre eux : à
nouveau, ceux-ci forment une droite : j'ai la
représentation graphique de ma nouvelle
fonction
Pour aller plus loin :
Ce nouvel exercice me permet de constater que :
Lorsque l'on ne m'impose pas de calcul
d'images, je peux prendre les valeurs de x que je désire pour tracer ma
représentation graphique : je
tâcherai alors de choisir les valeurs les plus
simples pour mon calcul
La
représentation graphique d'une fonction est une
droite : pour tracer une droite, j'ai besoin au minimum
de 2 points : chaque fois qu'on me
demandera de représenter graphiquement une
fonction, il me faudra donc prendre au moins 2 valeurs de
x pour le calcul de leur image
D'un autre côté et
inversement, 2 valeurs suffisent : il n'est pas
nécessaire d'en prendre d'avantage, sous peine et
risque de se perdre dans des calculs, qui seront
finalement superflus
Je remarque à chaque
représentation graphique, que mes valeurs de x, et leur image correspondante
constituent en fait des coordonnées de points pour
mon repère :
Lorsque je dis par exemple :
pour une valeur de x = 0 ; image =
(-1)je trace dans mon repère un point de
coordonnées (0; -1)
pour une valeur de x = 1; image =
2 je trace dans mon repère un point de
coordonnées (1; 2)
pour une valeur de x = 2; image =
5 je trace dans mon repère un point de
coordonnées (2; 5)
etc....
Je peux donc et par conséquent
établir une relation fonction/repère
f(x) 3x - 1, peut aussi
s'écrire pour mon repère :
C'est à dire pour une abscisse x donnée d'un point ,
j'obtiendrai y l'ordonnée
de ce même point par la fonction:
Cette relation est très utile, car elle me permet
d'obtenir facilement n'importe quelles coordonnées
de points par rapport à ma fonction :
génial non ??
Et voilà : je sais tout de la
représentation graphique d'une fonction
Mais au fait ??
|
Pourquoi représenter
graphiquement une fonction ?
|
Ce que je dois savoir :
Lorsque je détermine quelques coordonnées
de points pour le tracé de ma fonction dans un
graphique, je sais très bien que j'aurais pu de la
même façon calculer beaucoup d'autres
équivalences : des dizaines de points, des
centaines de points ......et ce jusqu'à une
infinité de points qui auraient
représenté graphiquement ma fonction
Ainsi et par conséquent, je dois savoir que la
droite représentative de ma fonction dans le
repère, obtenue par le tracé de 2 points
minimum, correspond en fait à l'ensemble des
points solutions pour ma fonction :
Je retiens donc cette règle :
|
Tous les points appartenant à la
droite de représentation d'une fonction
sont solutions de cette fonction
|
Et alors ?? Et bien, cela signifie par exemple, que
grâce au dessin, je peux donner :
Une valeur de y pour
une valeur de x donnée
Ou inversement
Comment ??
Et bien par la lecture des coordonnées de points
pardi !!
Représentez graphiquement la fonction f(x)
3x - 1
Ensuite, vous direz quelle est la valeur de la fonction
pour x = 1,5 ; vous effectuerez
une simple lecture puis vérifierez par le
calcul
J'ai déjà représenté
graphiquement cette fonction (ci-dessus) : sa
représentation graphique donne ceci :
Ensuite, je dois dire quelle est la valeur de la fonction
pour x = 1,5 :
Je comprends ce que l'on me demande :
donner la valeur de la fonction pour un x
donné, c'est donner le résultat du
calcul de cette fonction en remplaçant x par 1,5
Or on me demande ici de lire la réponse dans un
1er temps :
C'est à dire ?? Et bien étant donné
que la droite représente toutes les solutions de
la fonction, l'équivalence que je cherche devrait
s'y trouver :
Imaginez que j'aie tracé ma droite grâce
à la valeur de x = 1,5
J'aurais ainsi obtenu un point de coordonnée x = 1,5 ; y = ?
(avec y = image de x par la fonction)
Ce point aurait effectivement appartenu à ma
droite de représentation !!
La valeur y du point sera donc la valeur que je pourrai
lire sur l'axe des ordonnées, au point de
rencontre de x = 1,5 et de la
droite de représentation de la fonction :
Le point en question est dessiné en rose sur la
droite : je lis donc simplement ses coordonnées
:
(x = 1,5 ; y = environ 3,5)
Encore une fois, cette lecture aurait été
beaucoup plus précise grâce aux inter-lignes
du papier millimétré : je fais attention
également lors de ma lecture de bien respecter
l'échelle du graphique sur l'axe qui
m'intéresse :
Si je ne sais plus comment lire des coordonnées de
point sur un graphique, je retourne à la fiche :
Repères &
Coordonnées
Voici pour le principe de la lecture : ensuite, et c'est
le seul moyen de connaître la valeur exacte de la
fonction quand x = 1,5 : je
vérifie le résultat pour f(1,5) :
f(1,5) = 3 x 1,5 - 1 = 4,5 - 1 = 3,5
f(1,5) = 3,5 DONC y = 3,5
On a donc bien un point de représentation de la
droite de coordonnées (1,5 ; 3,5) : ma lecture
graphique n'était pas si mal que cela
Je fais une phrase de réponse :
"Pour x = 1,5, la
valeur de la fonction est 3,5"
Ou encore
f(1,5) = 3,5
Remarque : fonctions
et expressions avec des x
Les fonctions et les expressions
avec des x si j'ai bien compris
l'une et l'autre sont similaires de par leur
fonctionnement :
en effet, calculer f(1,5) revient exactement au
même lorsque dans l'expression 3x - 1, je remplace x par 1,5
Dans certains types de problèmes par exemple, je
peux être amenée à nommer les
inconnues :
C'est par exemple le cas de la mise en
équation d'un problème (car
une équation = expression avec des x) ou encore comme dans les exemples des
corrigés de sujet d'annales, lorsque l'on me
demande d'exprimer des longueurs de côté par
rapport à une longueur x
etc....
Je dois bien comprendre que les 2 notions sont
interdépendantes :
Prenons un exemple
:
Je suis au supermarché : il y a un promotion sur
les oranges:
Prix au Kilo : 3 euros - 1 euro de réduction sur
le prix global sera déduit en caisse : cela
signifie que pour n'importe quelle quantité
d'oranges achetées, je paierai : 3 euros x
quantité en Kgs - 1 euro
Et si j'appelle x la
quantité d'oranges achetées
Et bien quelle que soit la quantité, le calcul de
mon prix à payer se résume à : 3 x
x - 1
Ainsi si j'achète 2 kgs , je paierai : 3 x
2
- 1 = 5 euros
Ainsi si j'achète 3 kgs, je paierai : 3 x
3
- 1 = 8 euros
Ainsi si j'achète 4 kgs, je paierai : 3 x
4
- 1 = 11 euros
etc....
L'équation 3x
- 1 régit le rapport entre les
quantités de achetées et le prix à
payer
Quelle différence faisons nous alors avec la
fonction f(x) = 3x - 1
Et bien aucune : comparons les résultats :
|
Equation : 3x -
1
|
f(x) = 3x - 1
|
|
pour x = 2 ;
résultat de l'équation = 5
pour x = 3 ;
résultat de l'équation = 8
pour x = 4 ;
résultat de l'équation = 11
etc....
|
pour x = 2 ;
f(x) = 3 x
2 - 1 = 5
pour x = 3 ; f(x) = 3 x
3 - 1 = 8
pour x = 3 ; f(x) = 3 x
4 - 1 = 11
|
f(x) = 3x -
1 est donc en fait la fonction définie par : x = quantité en Kgs et son
image = prix à payer en euros
Je peux donc la représenter graphiquement,
Je saurai alors que :
Pour tout point appartenant à la
représentation graphique de la fonction, j'aurai
pour coordonnées :
( x = quantité de en Kgs ;
y prix à payer en €uros)
car je sais que l'image d'une fonction dans un
repère = y
Ainsi, le résultat de mon équation
pour un x donné, devient
le résultat de ma fonction pour la même
valeur de x
Après la mise en équation de mon
problème, on aurait pu alors me donner :
On note : f(x) la fonction
définit par : 3x - 1
Représentez graphiquement la fonction f(x) 3x - 1
Ensuite, vous direz le prix que vous devrez payer, si
vous achetez 1,5 Kgs : vous déterminerez ce prix
graphiquement, puis le vérifierez par le
calcul
Je comprends le problème :
|
On note : f(x) la
fonction définit par : 3x - 1
|
On a retranscris l'équation du
départ en fonction :
Je peux donc la
représenter graphiquement
J'aurai : x =
quantité de achetée en Kgs
image de x (c'est
à dire y) = prix
à payer en euros
|
|
vous direz le prix que vous devrez payer, si
vous achetez 1,5 Kgs : vous déterminerez
ce prix graphiquement, puis le vérifierez
par le calcul
|
Si x = quantité de
achetée en Kgs, je devrai donc lire sur
le graphique l'intersection de la
représentation de ma fonction avec x = 1,5 : j'obtiens de cette
façon la valeur y
du point de rencontre : cela tombe bien, car
y = prix à payer
en euros
|
J'ai trouvé par lecture et sur le dessin, y = 3,5
Retranscrit dans le contexte de mon problème, cela
veut donc dire que lorsque j'achète 1,5 Kgs
d'oranges, je dois payer 3,5 euros.
Bien sûr, je n'oublie pas de rédiger une
phrase de réponse :
Ainsi donc, mélangées dans un exercice,
fonctions et équations me permettent de :
Grâce à la fonction : pouvoir
représenter graphiquement mon
équation
Grâce à l'équation : nommer et
donner une valeur d'application à mes valeurs
x et y
des points de représentation de ma
fonction
Ce genre d'exercice est par exemple souvent
proposé dans la partie problème du brevet
des collèges : je peux d'ailleurs en voir un
nouvel exemple dans le corrigé N° 3
|
Et si c'était le cas
inverse ?
|
Explications :
Je viens de voir que avec une fonction donnée, je
peux :
- La représenter graphiquement
- Utiliser cette représentation
graphique pour lire des coordonnées de points,
et ainsi donner des valeurs à ma fonction
Et si maitenant, je n'avais pas une fonction,
mais une représentation graphique donnée
:
Exemple : On place dans un repère les
points A(2;5) et B (4;7)
La droite formée par A et B représente
graphiquement la fonction f(x)
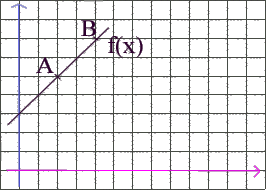
Et bien, je pourrais toujours utiliser cette
représentation pour lire des coordonnées de
points appartenant à la fonction :
Exemple : quand x = 1 ;
y = 4 : un point de la droite
représentative de la fonction a donc pour
coodonées (1 ,4) : la fonction f(x) a donc pour image 4, pour x = 1 Je
peux écrire : f(1) = 4 etc....
Par contre, est-ce que je peux vérifier ces
données par le calcul ?? ET BIEN NON ....
Pourquoi ?? Et bien simplement parce que l'exercice ne me
donne qu'un graphique : je n'ai donc pas
l'équation de la droite, la fonction
Alors je crois que dans ce cas et tout bêtement, on
pourra me demander :
"Déterminez la fonction f(x)"
Oh la la, cela se complique !!
Et bien non, c'est tout à fait logique :
J'ai une fonction Je
dois la représenter graphiquement
J'ai une représentation graphique Je
dois trouver sa fonction ....
Règle : la fonction
représentée sur le graphique peut
être déterminée à son tour de
2 manières différentes :
- Par le calcul
- Et par lecture graphique
Mais pour cela, et pour les 2 méthodes, il
me faut un peu de
vocabulaire :
Vous allez, voir, vous allez comprendre :
En réalité, dans sa
formulation, une fonction contient des
éléments repérables sur le dessin,
ou qui peuvent se déterminer par le calcul
grâce à des coordonnées de points :
cet indice est précieux pour notre recherche
n'est-ce pas ?,
Regardons cela de plus près :
Si je reprends mes deux exemples de fonctions
vues ci-dessus :
f() =
4 + 2
f() =
3 - 1
Je constate en réalité que les 2
fonctions sont formées sur le même moule
:
un nombre multiplié par
+/- un autre
nombre
f() =
3 - 1
a = 3
Le coefficient directeur de la droite
représentative de f(x)= 3
Qu'est-ce que cela implique ?
Et bien, sur mon dessin, je dois avoir une pente de
3 (graduations) entre les différents points
de ma droite
Regardez plutôt sur le dessin
: Je me déplace bien de 3 graduations dans
le sens de la hauteur pour arriver à la
prochaine rencontre de la droite : ma "pente est
donc bien de 3"
|
|
Règle :
si a est négatif : la droite de
représentation de la fonction est descendante 
si a est positif : la droite de représentation de
la fonction est ascendante (monte)
Et l'ordonnée à l'origine, qu'est-ce que
c'est ? Et bien je crois qu'elle porte bien son nom :
c'est en fait la valeur de l'ordonnée lorsque la
droite représentative de la fonction passe par
l'origine
En résumé, c'est la valeur de la fonction,
lorsque x = 0 ; c'est pour cela en
réalité que cette valeur correspond dans ma
formule de fonction au nombre b
f() =
3 - 1
b = - 1
L'ordonnée à l'origine de la droite
représentative de f(x) est donc = - 1
Logique car f(0) = 3 x 0 - 1 = - 1
Qu'est-ce que cela implique ?
Et bien, sur mon dessin, l'ordonnée à
l'origine est donc le point de la droite qui a pour
coordonnées (0 ; - 1)
Le nombre b de la fonction sera
donc toujours la valeur de l'ordonnée, quand
la droite rencontre l'axe d'origine
|
|
Résumons nous :
Je viens de montrer que les nombres a et b dans
formulation de la fonction f(x) = ax + b, pouvaient se lire aisément
sur le dessin :
Pourquoi alors ne pas en profiter pour lire ces nombres
quand justement on nous demande de donner la formule de
la fonction (et qu'on ne l'a pas bien sûr) :
Reprenons notre exemple de tout à l'heure :
On a placé dans un repère les points A(2;5)
et B (4;7)
La droite formée par A et B représente
graphiquement la fonction f(x) :
je dois donner la fonction f(x)
Conformément à ce que je viens de voir, je
pars du principe que ma fonction va s'écrire :
f(x) = ax +
b
avec a : pente de la droite
et b : valeur de la fonction sur l'axe des
ordonnées quand sa représentation rencontre
l'origine
Je regarde ces éléments sur le dessin :
- Pour ce qui est de la pente : je me
déplace verticalement de 1
graduation pour rencontrer de nouveau
la droite : mon coefficient directeur sera positif car la
droite monte
J'aurai donc : coefficient directeur de la droite =
+ 1
- Pour ce qui est de l'ordonnée à
l'origine :
Quel est la valeur de y
lorsque la droite rencontre l'axe du repère
(origine) ?
Réponse : indiquée par la flèche sur
le dessin : y = 3
J'aurai donc : ordonnée à l'origine de la
droite = + 3
Et si : f(x) =
ax + b
avec a : pente de la droite
et b : ordonnée à l'origine de la
droite
Alors, la fonction f(x) aura pour formule : 1 x + 3
f(x) = x + 3
J'ai ainsi obtenu la fonction représentée
par ma droite
Je peux alors vérifier :
que mes 2 points A et B vérifient
bien cette expression : en effet, puisqu'ils
appartiennent à la droite de
représentation, leurs coordonnées
doivent donc vérifier la fonction
|
A (2 ;5 ) : x = 2
; y = 5
|
f(2) = 2 + 3 = 5
donc y = 5
La représentation de la fonction f(x) = x +
3 comprend bien un point de coordonnées
(2;5) : mon point A appartient donc bien
à la droite
|
|
B (4 ;7 ) : x = 4
; y = 7
|
f(4) = 4 + 3 = 7
donc y = 7
La représentation de la fonction f(x) = x +
3 comprend bien un point de coordonnées
(4;7) : mon point B appartient donc bien
à la droite
|
L'écriture de ma fonction obtenue par lecture
graphique semble correcte
Je l'ai dit tout
à l'heure : ma fonction peut se lire
graphiquement, mais peut aussi se calculer : le calcul
est un moyen sûr et pratique d'arriver à
un résultat correcte surtout quans la lecture
graphique est difficile (rappelez-vous tout à
l'heure : nous avons laissé tombé le 1er
exemple de fonction car sa lecture était trop
imprécise, à cause de
l'échelle)
Comment je calcule l'équation d'une
fonction ?
Qui dit calcul dit formules de calcul : je devrai donc
apprendre la méthode....et les formules
Principe :
Le calcul de l'équation d'une fonction va reposer
sur les coordonnées des points formant la
représentation gaphique de la fonction
Et bien oui !! On a vu tout à
l'heure que tous les points appartenant à la
droite de représentation d'une fonction sont
solutions de cette fonction
Si ces points sont solutions cela signifie bien sûr
que leurs coordonnées vérifient
l'équation de la fonction
Ainsi, pour une fonction de type ax + b et un point A de
coordonnées x = 2 et y = 5, ma fonction devient :
5 = a x 2 + b ( 5
= 2a + b)
C'est à dire : l'image de x = 2 par la fonction
est 5 (comme nous l'avons fait tout à l'heure dans
notre recherche de points)
Et donc pour mon point B de coordonnées x = 4 ; y = 7,
j'aurai :
7 = a x 4 + b ( 7
= 4a + b)
Je sais que ces 2 points appartiennent à la droite
de représentation de ma fonction : c'est donc eux
qui vont me permettre de calculer l'équation de
cette fonction, en déterminant par le calcul a et
b
Comment ? Et bien deux solutions sont possibles :
Je sais que mon point A me permet d'écrire
la fonction : 5 = 2a + b et mon point B : 7 = 4a + b
Ces formules de fonction sont 2 équations dont il
me manque 2 valeurs : a et b
Je connais en algèbre une technique pour
déterminer ces valeurs pas le calcul :
2 équations + 2 inconnues =
résolution d'un système
d'équations
Bien sûr, si cela ne vous dit rien,
retournez à la
fiche correspondante
Je mets donc mes 2 équations en système
:
Je résous le système par annulation : je
multiplierai ma 2ème équation par (-1) pour
obtenir - b et ainsi l'annuler :
Mon système devient : 
Je fais l'addition des 2 équations : 5 - 7 = 2a -
4a (b et - b s'annulent)
Je n'ai alors plus qu'une seule inconnue : je la
calcule
5 - 7 = 2a - 4a
- 2 = - 2a
a =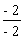 
a = 1
J'ai trouvé ma première inconnue : je peux
alors la remplacer dans les équations :
A : 5 = 2a + b ; 5 = 2 x 1 + b ; b = 5 - 2 ; b = 3
B : 7 = 4a + b ; 7 = 4 x 1 + b ; b = 7 - 4 ; b = 3
J'ai donc pour résultats du système
: a = 1 ; b = 3
Si donc la formule de ma fonction est ax + b alors ma fonction a pour
équation :
f(x) = (1)x
+ 3
f(x) = x +
3
Et voilà : la formule de ma fonction a
été trouvée par le calcul
2ème solution :
Il existe une formule de calcul du coefficient
directeur de la droite de représentation de la
fonction à partir toujours des
coordonnées de 2 points formant cette
droite
Rappel : le coefficient directeur dans une
fonction de formule ax + b
correspond au nombre a
Voici la formule de calcul de ce coefficient :
a =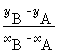 
|
C'est à dire : "Ordonnée du point B
- ordonnée du point A
sur (ou divisé par)
abscisse du point B - abscisse du point
A"
Je dois donc apprendre cette formule, la comprendre et la
savoir (comme toutes les formules)
Application sur mon exemple :
Mes points A de coordonnées x = 2 et y = 5,
et B de coordonnées x = 4
et y = 7, appartenant à la
droite de représentation de la fonction, je vais
donc pouvoir utiliser leurs coordonnées pour
calculer le coefficient directeur de cette droite)
J'applique la formule que je viens de voir :
a =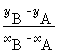
Je remplace les lettres par les coordonnées de mes
points ; la formule devient :
a =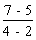 
7 - 5 = 2 ; 4 - 2 = 2
a est donc égal à  =
1
J'ai le coefficient directeur de ma droite de
représentation
Et alors : à quoi cela va-t-il me servir pour le
calcul de l'équation de ma fonction ??
Et bien à ce stade de mon calcul, je me trouve en
réalité au même point qu'avec mon
système, lorsque j'ai dégagé ma
première inconnue :
Puisque ma fonction a pour formule ax + b et que mes points A et B
appartiennent à la droite représentative de
la fonction, alors les coordonnées de ces points
vérifient l'équation de la fonction :
DONC A : 5 = 2a + b et B : 7 = 4a + b
Il ne me sera alors pas plus diffcile que tout à
l'heure, maintenant que je connais a de trouver b
Il me suffit de remplacer a dans les équations
:
A : 5 = 2a + b ; 5 = 2 x 1 + b ; b = 5 - 2 ; b =
3
B : 7 = 4a + b ; 7 = 4 x 1 + b ; b = 7 - 4 ; b = 3
J'obtiens bien la même chose que tout à
l'heure a = 1 ; b = 3
Ma fonction s'écrit bien : f(x) = x + 3
Et voilà pour ce qui est de la
détermination d'une fonction par le calcul : 2
solutions pour un calcul (avec tout ça, on a au
moins intérêt à ce que le calcul soit
juste !!).
Comme d'habitude, chacun choisira la méthode de
calcul qui lui convient le mieux ......
Voilà également pour ce qui concerne les
fonctions : nous avons fait le tour de ce qu'on peut nous
demander sur les fonctions affines et
linéaires........
Comment ?? J'ai oublié de vous parler des
fonctions affines et linéaires ??
Pas de panique ......Vous allez voir c'est très
simple :
Est appelée fonction affine une fonction qui a
pour formule ax + b (avec a =
coefficient directeur et b = ordonnée à
l'origine)
Cela rassure : tout ce que viens de vois concerne en fait
les fonctions affines :
Ainsi et pour reprendre mes exemples :
f() =
4 +2 est une fonction
affine (forme ax + b avec
coefficient directeur = 4 et ordonnée à
l'origine = 2)
f(x) 3x - 1 est une
fonction affine (forme ax + b avec
coefficient directeur = 3 et ordonnée à
l'origine = - 1)
Et enfin :
f(x) = x +
3 est une fonction affine (forme ax + b avec coefficient directeur = 1 et
ordonnée à l'origine = 3)
Mais alors ....Et les fonctions linéaires....??!!
Cela voudrait dire que l'on en a pas parlé du tout
??
Et bien encore une fois pas de panique.....
Sachez que la seule différence entre les 2 types
de fonctions, est que la fonction linéaire
ne possède pas d'ordonnée
à l'origine
DONC :
Au niveau de sa formule : elle ne
possèdera pas de b
Une fonction linéaire s'écrit
donc : f(x) =
ax
Au niveau de sa représentation
graphique : sa droite de représentation ne
coupera donc pas l'axe des ordonnées en une
certaine valeur (quand x sera
égal à 0, y sera
donc aussi égal à 0)
Implication directe : la droite de
représentation d'une fonction linéaire
passera donc toujours par le point de
coordonnées (0; 0), c'est
à dire par l'origine du repère
Pour sa représentation graphique :
rien ne change ; on utilisera cette fois la formule y = ax
pour placer des points
1 avantage cependant : puisqu'une fonction
linéaire implique expressément que sa
représentation graphique passe par l'origine, il
me suffira de déterminer les coordonnées
d'un seul point pour obtenir la droite
Pour la détermination de son
équation à partir de sa
représentation graphique :
Par la
lecture : comme je l'ai dit, si la droite passe
par l'origine, alors la fonction est linéaire :
elle aura donc pour formule ax
et il me suffira de lire a (coefficient directeur)
Par la lecture : toujours en
raison de cette absence du b dans sa formule, cette
fois, la méthode de calcul par le
système d'équations devient inutilisable
: il me suffira alors de résoudre simplement
une équation ou encore d'utiliser la
2ème méthode de calcul du coefficient
directeur pour trouver a)
OUI . BON . D'ACCORD; Puisque c'est vous, je vous donne
quand même un exemple de ce type de fonction
|
J'ai la fonction : je dois construire
sa représentation graphique
|
J'ai la représentation
graphique de la fonction : je dois
déterminer son
équation
|
|
f(x ) = 3x
C'est une fonction linéaire car elle
est de la forme ax
Pour tracer sa représentation
graphique, je sais que : la droite de
représentation passera pas le point O du
repère (origine) il me suffit donc de
déterminer les coordonnées d'1 seul
autre 2 points : j'utilise pour cela la
formule y = 3x
y = 3 x 1 =
3
J'ai mes 2 points : le point O du repère et
le point de coordonnées (1 ;3) : je peux
tracer ma représentation
Echelle du repère : 1 unité = 2
graduations
Je pourai ensuite et normalement lire des
coordonnées de points appartenant à
cette fonction
|
A (1;1)
La droite de représentation de cette
fonction passe par l'origine du repère :
c'est donc la représentation d'une fonction
linéaire de formule :
f(x ) = ax
Il me suffit donc de déterminer a
:
1. par la lecture
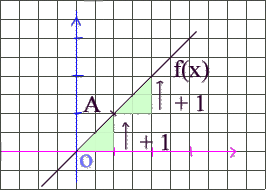
Droite ascendante : donc
coefficient positif
Je monte de 1 graduation : mon coefficient
directeur est donc égal à + 1 a = 1
Ma fonction linéaire a donc pour formule
f(x ) = x
Je le vérifie par le
calcul
Le point A de coordonnées x = 1 et y
= 1 appartient à la représentation de
la fonction : ses coordonnées
vérifient donc l'équation y = ax avec
1 = a x 1
DONC : a =  = 1
Avec la formule de calcul du coefficient
directeur :
C'est à dire : "Ordonnée du point B
- ordonnée du
point A sur (ou divisé par)
abscisse du point B - abscisse du
point A"
Je prends pour équivalent du point B le
point O (0;0)
Ainsi ma formule devient :  =  = 1
|
Et voià pour la fonction linéaire
Remarque : la fonction linéaire est la
fonction de la proportionnalité par excellence :
en effet, j'ai vu dans la fiche sur la
proportionnalité que :
"deux valeurs sont proportionnelles si on les multiplie
ou divise toujours par le même nombre"
Ainsi, j'aurais pu résumer la
proportionnalité en :
Soit deux valeurs x et y données : ces deux valeurs sont
proportionnelles si et seulement si on a:
y = a x x
(le a s'appelle alors le coefficient de
proportionnalité)
Autrement dit la définition même de
notre fonction linéaire
ATTENTION DONC : ne vous étonnez pas si on vous
demande dans un exercice de proportionnalité
(vitesse, échelles, pourcentages) de
représenter les valeurs proportionnelles dans un
graphique : vous saurez alors qu'il faut passer de la
proportionnalité à la
fonction linéaire......
ET PAR OPPOSITION : si on vous donne des valeurs qui ne
sont pas proportionnelles, vous saurez qu'il faut passer
de ces valeurs à la fonction
affine ....!!
ALORS ....TOUT COMPRIS ???
|
