|
LES POURCENTAGES
|

|
Ah,
ces fameux pourcentages !! Qui n'a jamais bloqué sur
cette technique qui est pourtant le cas par excellence de la
proportionnalité ?? C''est le cas aussi que l'on
rencontre le plus souvent, et qui peut être
adapté aux situations les plus variées : donc
il vaut mieux le connaître non ??
|
Un
pourcentage : qu'est-ce que c'est ?
|
On le retrouve partout dans notre vie quotidienne :
poourcentages de réduction, pourcentages
d'augmentation sur des prix, des quantités,
pourcentages d'effectifs à l'école,
pourcentages de réussite à un examen
etc....etc...
La représentation écrite du pourcentage : le
signe %
Exemples : Il y a eu cette année 79
% (se lit : soixante-dix neuf pour cent) de
réussite au brevet des collèges - Pendant
les soldes, j'ai eu cet article à moins 30 % (se
lit trente pour cent) etc....
Que veulent dire 79 % ? ; 30 % ?
Et bien simplement que :
79 % de réussite 79 élèves
sur
cent
ont réussi leur examen 79 élèves
sur
cent
ont réussi leur examen
30 % de réduction  J'ai eu une réduction
de
30 €
sur
100 €
du prix de l'article etc..... J'ai eu une réduction
de
30 €
sur
100 €
du prix de l'article etc.....
Règle : Exprimer un pourcentage, c'est donc
ramener la valeur dont il est question par rapport au
nombre 100 : on le dit d'ailleurs lorsqu'on lit le
pourcentage :
30 % : se lit trente pour cent : veut dire "pour cent,
j'en ai trente"
79 % : se lit soixante-dix-neuf pour cent : veut dire
"pour cent, j'en ai soixante-dix-neuf"
etc....
J'ai donc ici une notion de part : le total de ma valeur
est ramené à un total de 100, et la part de
cette valeur est exprimée par le nombre qui se
trouve devant le pourcentage : il faut donc bien
comprendre quelle est la valeur en question :
Exemple
1 : 79
% de réussite à l'examen : cela signifie
que 79 éléves sur 100 ont réussi
l'examen : Je peux faire ainsi le tableau de
proportionnalité suivant :
|
total
des élèves
|
100
|

|
|
élèves
ayant réussi l'examen
|
79
|

|
J'ai retranscris la signification de mon pourcentage (sur
un total de 100 élèves, 79 ont
réussi l'examen) : mes valeurs sont bien
proportionnelles : en effet, si j'ai un total de 200
élèves, le pourcentage implique que j'ai
deux fois la base cent, donc en proportions, 2 fois plus
d'élèves qui ont réussi à
l'examen etc.....
Je peux alors par rapport à ces données, et
grâce à ce tableau, répondre à
deux types de questions :
- Je donne un
total d'élèves de 3è, et
grâce au pourcentage, je cherche combien ont eu
leur examen
- Ou au
contraire, je donne un nombre d'élèves
de 3è qui ont réussi leur examen, et
grâce au pourcentage, je cherche combien
d'élèves au total ont passé
l'examen
Enoncé 1 :
[L'année
dernière, 300 élèves de 3è
du collège X.ont passé le brevet des
collèges : le collège a
enregistré un taux de réussite de 79 % :
combien d'élèves de 3è ont eu
leur examen ??]
Méthode :
Je mets les données dans mon tableau :
1. Traduction du pourcentage
2. On me donne une nouvelle indication; : total des
élèves = 300 : je remplis une nouvelle case
"total des élèves"
|
total
des élèves
|
100
|
300
|
|
élèves
ayant réussi l'examen
|
79
|
?
|
Il ne me reste plus qu'à faire le calcul : je fais
le produit en croix :
100 x ? = 79 x 300
79 x 300 = 23700
100 x ? = 23700
? = 23700 ÷ 100
? = 237
Je mets la valeur calculée dans le tableau :
|
total
des élèves
|
100
|
300
|
|
élèves
ayant réussi l'examen
|
79
|
237
|
Je fais une phrase de réponse à mon
problème : "237 élèves de
3è du collège X ont eu leur
examen"
Enoncé 2 : le problème
inverse
[L'année
dernière, 320 élèves de 3è
du collège X.ont obtenu leur examen du brevet
des collèges : cela représentait un taux
de réussite de 79 % : combien
d'élèves de 3è ont passé
l'examen ??]
Je mets les données dans mon tableau :
1. Traduction du pourcentage
2. On me donne une nouvelle indication; cette fois-ci, ce
n'est plus le total des élèves mais le
nombre des élèves ayant réussi leur
examen = 320: je remplis une nouvelle case
"élèves ayant réussi l'examen"
|
total
des élèves
|
100
|
?
|
|
élèves
ayant réussi l'examen
|
79
|
320
|
Il ne me reste plus qu'à faire le calcul : je fais
le produit en croix :
100 x 320 = 79 x ?
100 x 320 = 32000
79 x ?= 32000
? = 32000 ÷ 79
? = 405,06
Vu qu'il s'agit au départ d'un nombre
d'élèves, je dois arrondir au nombre entier
le + proche = 405
Je mets la valeur calculée dans le tableau :
|
total
des élèves
|
100
|
405
|
|
élèves
ayant réussi l'examen
|
79
|
320
|
Je fais une phrase de réponse à mon
problème : "405 élèves de
3è du collège X ont passé
l'examen"
Autre
cas de figure très souvent
rencontré :
|
Augmentations et diminutions par
un pourcentage
|
C'est le cas de mon exemple : "réduction sur un
article : - 30 %"
Il est important de bien comprendre cette situation car
nous y sommes souvent confrontés :
Que veut dire l'étiquette posée sur un
article : - 30 % ??
Et bien simplement que sur la base d'un prix de 100 €, le
magasin accorde une réduction de 30 € sur
l'article :
Je peux faire ainsi le tableau de proportionnalité
suivant :
|
Prix
de l'article en €
|
100
|

|
|
réduction en
€
|
30
|

|
J'ai retranscris la signification de mon pourcentage
(pour un article étiqueté à 100 €,
j'ai une réduction de 30 €) : mes valeurs sont
bien proportionnelles : le calcul de ma réduction
va en effet augmenter ou diminuer en fonction du prix
étiqueté : si un article est
étiqueté 200 €, j'aurai le double de
réduction , soit 30 x 2 = 60 € etc....)
Je peux alors par rapport à ces données, et
grâce à ce tableau, répondre à
deux types de questions :
- Je donne un
prix étiqueté avant réduction :
je cherche de combien mon article sera
réduit
- Ou au
contraire, je connais la réduction : je vais
alors chercher le prix de l'article
étiqueté au départ :
Enoncé 1 :
[Je viens de
recevoir un bon de réduction sur catalogue : -
30 % à valoir sur un article. Cette petite robe
me plaît bien : elle coûte 24 € ; avec la
réduction, elle ne devrait pas me coûter
trop cher !!]
Mais au fait,
à combien va se monter la réduction sur un
prix de 24 € ??
Je mets les données dans mon tableau :
1. Traduction du pourcentage
2. On me donne une nouvelle indication; : prix de
l'article = 24 € : je remplis une nouvelle case "Prix de
l'article en €"
|
Prix
de l'article en €
|
100
|
24
|
|
réduction en
€
|
30
|
?
|
Il ne me reste plus qu'à faire le calcul : je fais
le produit en croix :
30 x 24 = 100 x ?
30 x 24 = 720
100 x ? = 720
?= 720 ÷ 100
? = 7,2
Je mets la valeur calculée dans le tableau :
|
Prix
de l'article en €
|
100
|
24
|
|
réduction en
€
|
30
|
7,2
|
Je sais maintenant que une réduction de 30 % sur
24 € représente une réduction de 7,2 €
Résultat : si je commande,
combien vais-je payer ma robe ??
Et bien : 24 - 7,2 = 16,80 €
Remarque : la question aurait très
bien pu être : combien vais-je payer ma robe
après réduction :
2 solutions alors s'offrent à moi :
 Soit, comme je viens de le faire, je
calcule le montant de ma réduction sur mon
article et le retranche de son prix Soit, comme je viens de le faire, je
calcule le montant de ma réduction sur mon
article et le retranche de son prix
 Soit dans l'interprétation de mon
pourcentage, je traduis ce qu'il me reste de mon prix
et non plus ma réduction : Soit dans l'interprétation de mon
pourcentage, je traduis ce qu'il me reste de mon prix
et non plus ma réduction :
Explications :
si 30 % de réduction signifie que sur un article
étiqueté 100 €, j'ai 30 € de
réduction : ne puis-je pas dire alors que pusique
j'ai 30 € de réduction, il me restera 70 €
à payer ?? (100 - 30 = 70)
Ce sont ces valeurs cette fois que je vais inscrire dans
mon tableau :
"Sur un article étiqueté 100 € il me
restera à payer 70 € après la
réduction" : mes intitulés de ligne
deviennent alors :
|
Prix
de départ de l'article en €
|
100
|
24
|
|
Prix
de l'article en € après
réduction
|
70
|
?
|
Je sais alors que mon calcul aboutira directement au prix
de l'article à payer après réduction
:
Je fais le produit en croix :
70 x 24 = 100 x ?
70 x 24 = 1680
100 x ? = 1680
?= 1680 ÷ 100
? = 16,80
Résultat : Le prix de l'article après
réduction est bien de 16,80 € : à chacun de
choisir sa méthode !!
Et si on avait augmenté le prix ?? Et bien de la
même façon, j'aurais :
Méthode N°
1 :
Calculé la valeur de l'augmentation dans mon
tableau, puis je l'aurais additionnée à mon
prix de départ :
Exemple : augmentation de 30
% sur 24 € = 7,2 € d'augmentation
Donc prix après augmentation : 24 + 7,2 = 31,2
€
Méthode N°
2 :
Calculé directement le prix à payer
après l'augmentation en ajoutant la valeur de
l'augmentation au prix de départ 100 :
Exemple : augmentation de 30
% = 100 + 30 = 130
Prix à payer après augmentation =
130
donc dans mon tableau :
|
Prix
de départ de l'article en €
|
100
|
24
|
|
Prix
de l'article en € après
augmentation
|
130
|
?
|
Calcul par le produit en croix : 24 x 130 / 100 = 31,20
€
31,20 €
est effectivement le prix à payer après
augmentation
Enoncé 2 :
[Sur mon ticket
de caisse je lis : réduction - 30 % = 10,20
€.
Mais zut !! J'ai perdu l'étiquette de la robe
que je viens d'acheter : et je ne me souviens plus
combien elle coutait au départ : le
problème ici est donc inverse : je connais le
montant de ma réduction : je dois chercher le
prix de départ ]
Je mets les
données dans mon tableau :
1. Traduction du pourcentage
2. On me donne une nouvelle indication; :
réduction = 10,20 € : je remplis une nouvelle case
"Réduction en €"
|
Prix
de l'article en €
|
100
|
?
|
|
réduction en
€
|
30
|
10,20
|
Il ne me reste plus qu'à faire le calcul : je fais
le produit en croix
10,20 x 100 = 30 x ?
10,20 x 100 = 1020
? = 1020 ÷ 30
? = 34
Je mets la valeur calculée dans le tableau :
|
Prix
de l'article en €
|
100
|
34
|
|
réduction en
€
|
30
|
10,20
|
Je sais maintenant que si avec une réduction de 30
%, j'ai économisé 10,20 € c'est que le prix
de la robe était de 34 € au départ : je
n'ai plus besoin de retrouver l'étiquette : j'ai
la réponse à ma question !!
Remarque
:
regardons bien les différentes opérations
de calcul réalisé :
Pour un pourcentage donné : soit
 J'ai ma valeur de départ :
je recherche la part que le pourcentage représente
: J'ai ma valeur de départ :
je recherche la part que le pourcentage représente
:
Je fais toujours la même opération :
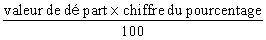
Exemple : 79 %
de 300 élèves =  =
237 =
237
Du coup et grâce aux propriétés des
fractions, je peux écrire aussi :  x
300 (300/1) : l'écriture du pourcentage est alors
sous forme de fraction : 79 % = x
300 (300/1) : l'écriture du pourcentage est alors
sous forme de fraction : 79 % = 
ou encore 0,79 x 300 (écriture du pourcentage sous
forme décimale si je calcule la fraction  =
79 ÷ 100 = 0,79) =
79 ÷ 100 = 0,79)
Inversement
 J'ai la valeur de ma part : je
dois trouver grâce au pourcentage la valeur de
départ : J'ai la valeur de ma part : je
dois trouver grâce au pourcentage la valeur de
départ :
Je fais là aussi toujours la même
opération :
Exemple : 320 élèves
représentent 79 % du total ;
Pour trouver le total de 405 , j'ai bien fait
l'opération : 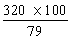
Ces formules, une fois que le pourcentage est compris,
peuvent me permettre de calculer plus rapidement : mais
attention : je dois toujours me souvenir du
fonctionnement du tableau de proportionnalité au
cas où ces formules me fassent défaut : je
pourrai alors ainsi facilement les retrouver....
|
Répartition grâce
à un pourcentage
|
Le pourcentage étant comme je vous l'ai dit
une part
de quelque chose, il peut, au même titre que
les fractions, être utilisé dans un
problème de répartition :
Ce type de problème est couramment
rencontré, et souvent les élèves ne
sont pas beaucoup inspirés (pas plus que pour les
problèmes avec des fractions d'ailleurs) :
Exemple
d'énoncé :
[Dans un
collège, les  des
élèves sont demi-pensionnaires, 30 % des
élèves sont internes, et les 72
élèves restants sont externes : calculer
le nombre d'élèves inscrits dans cet
établissement] des
élèves sont demi-pensionnaires, 30 % des
élèves sont internes, et les 72
élèves restants sont externes : calculer
le nombre d'élèves inscrits dans cet
établissement]
Je
réfléchis :
Le nombre total
des élèves inscrits est égal au
nombre des demi-pensionnaires + le nombre des internes +
le nombre des externes
Jusque
là rien de bien compliqué
Total = demi-pensionnaires +
internes + externes
Je connais le
nombre des externes : 72
Et à côté de cela, on me donne
:
1/ La part des
élèves demi-pensionnaires :  du total
du total
2/ La part des élèves internes : 30 % du
total
Voici
schématiquement la
répartition :

- Si je me
souviens bien de la signification d'une fraction (sinon,
je révise) je sais que prendre
 du
total signifie que : du
total signifie que :
Je divise le
total en 5 parties égales et j'en prends 3
:
j'ai donc :  x 3 = x 3 =  x total = 0,6 x total (car 3
÷
5 =
0,6)
x total = 0,6 x total (car 3
÷
5 =
0,6)
- Puisque je
viens de voir les pourcentages, je connais aussi leur
signification : je sais que prendre 30% du total des
élèves signifie que :
Sur 100
élèves, j'en prendrai 30 : donc sur le
total, j'en prendrai : 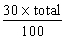 , ou encore , ou encore  x total ou encore 0,3 x total
x total ou encore 0,3 x total
Je me souviens
de mon tableau de proportionnalité et du produit
en croix à effectuer :
|
total
des élèves
|
100
|
total
|
|
total
des élèves internes
|
30
|
?
|
J'ai donc bien : 30 x total = 100 x ?
et donc ? = 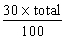
Je suis bien avancée : je me retrouve donc avec
:
total = 0,6 x total + 0,3 x total + 72
Mais comment alors obtenir mon total ??
Ah heureusement que je connais quelques notions de
mathématiques, et que je sais que pour trouver une
valeur inconnue, j'ai une solution bien pratique : la
résolution d'équation : (si je ne m'en
souviens pas, comme d'habitude, je révise)
Et si j'appelais x mon total d'élèves,
j'aurais alors :
x = 0,6 x x + 0,3 x x + 72
Je résous l'équation : x = 0,6x + 0,3x +
72
x - 0,6x - 0,3x = 72
x - 0,6x - 0,3x = 0,1 x
0,1 x = 72
x = 
x = 720 (72 ÷ 0,1 = 720)
Mon total d'élèves serait donc de 720 : je
vérifie en calculant maintenant la
répartition chiffrée des
demi-pensionnaires, externes, et internes :
demi pensionnaire =  du total donc du total donc  de
720 = de
720 =  = 432 = 432
internes = 30 % du total donc 30 % de 720 = =
216 =
216
externes = 72 : je connaissais déjà le
nombre
Est-ce que l'addition de 432, 216 et72 donne bien un
total de 720 ?
Réponse OUI : ma répartition est
effectuée, mes valeurs manquantes sont
chiffrées : mon problème est résolu
!
|
Opération inverse :
recherche d'un pourcentage
|
Cette fois je ne connais pas la valeur en pourcentage que
représente ma part sur mon total : je dois la
rechercher
Enoncé type :
[J'ai
acheté 1 robe en soldes : elle coûtait au
départ 24 € ; j'ai eu une réduction de
5,40 € sur son prix : Quel est le pourcentage de la
réduction qui m'a été
accordé ??]
Comme d'habitude, je marque mes données dans un
tableau :
y note les informations données par
l'énoncé : J'ai obtenu 5,40 € de
réduction sur un article étiqueté
à 24 € : cette fois-ci je ne connais pas le
pourcentage
|
Prix
de l'article en €
|
24
|

|
|
réduction en
€
|
5,40
|

|
Je sais que par définition un pourcentage est
toujours une part ramenée à une valeur
totale initiale de 100 : je vais donc remplir une
nouvelle case "prix de l'article en €" = 100
|
Prix
de l'article en €
|
24
|
100
|
|
réduction en
€
|
5,40
|
?
|
J'ai 3 valeurs sur 4 : il ne me reste plus qu'à
effectuer le produit en croix :
5,40 x 100 = 24 x ?
5,40 x 100 = 540
540 = 24 x ?
? = 540 ÷ 24
? = 22,50
Je mets le résultat de mon calcul dans le tableau
:
|
Prix
de l'article en €
|
24
|
100
|
|
réduction en
€
|
5,40
|
22,50
|
Je viens de calculer la valeur de la réduction
pour 100 € ; je viens donc de calculer la valeur de mon
pourcentage de réduction :
Si j'ai 5,40 € de réduction sur un article
étiqueté 24 €, j'aurai alors eu 22,50 % de
réduction
Et voilà pour le calcul du pourcentage : cela doit
paraître simple, si on a parfaitement compris le
tableau de proportionnalité type des pourcentages
: car à force, c'est toujours la même chose
!!
Remarque : j'aurais très bien pu
avoir aussi un énoncé du genre :
"Une robe dont le prix marqué est 24 € a
été payée après remise 18,60
€ : calculer le pourcentage de remise accordé sur
cet article"
Je devrai
d'abord calculer le montant de la remise : 24 - 18,60
= 5,40 €, pour pouvoir calculer ensuite le pourcentage
de cette remise, comme ci-dessus
Conclusion :
Quelle opération devont-nous effectuer pour
calculer la valeur d'un pourcentage ??
 ou encore : ou encore : 
(5,40 ÷ 24) x 100
5,40 ÷ 24 = 0,225
0,225 x 100 = 22,5
Pourcentage : 22,50 %
|

