|
LES INEQUATIONS
|

|
|
Qu'est-ce
qu'une inéquation ?
|
Dans la fiche
précédente, j'ai vu q'une équation
était une égalité composée de
différents calculs avec différents termes
(dont au moins une inconnue), et que résoudre une
équation revenait à calculer la valeur de
l'inconnue de l'égalité (inconnues  , y, a, b, t ....) , y, a, b, t ....)
Pourquoi ai-je besoin de me rappeler la définition
d'une équation ? Et bien tout simplement parce que
pour l'inéquation, c'est la même
système. La différence ? Si
l'équation est une égalité,
l'inéquation est une
inégalité : comme l'équation,
l'inéquation est composée de
différents calculs avec différents termes,
dont au moins une inconnue.
Différence entre
égalité et inégalité:
 Egalité : symbolisée par le
signe = ; Lorque je résouds une
équation, mon inconnue correspond à
une valeur et une seule Egalité : symbolisée par le
signe = ; Lorque je résouds une
équation, mon inconnue correspond à
une valeur et une seule
ex :
 - 2 = 0 ; x = 2 ; la valeur
de - 2 = 0 ; x = 2 ; la valeur
de  est 2 est 2
 Inégalité :
symbolisée par les signes < ; > ; Inégalité :
symbolisée par les signes < ; > ;  ; ; ; Lorque je résouds une
inéquation, mon inconnue peut-être
plusieurs valeurs. La solution de mon
inéquation est un ensemble de
valeurs. ; Lorque je résouds une
inéquation, mon inconnue peut-être
plusieurs valeurs. La solution de mon
inéquation est un ensemble de
valeurs.
C'est la
différence fondamentale entre une
égalité et une
inégalité:
Je
comprends :
Etudions les
signes que je peux rencontrer dans une
inéquation : ce sont :
< : se lit "strictement inférieur
à "ou "strictement plus petit
que"
> : se lit "strictement supérieur
à" ou "strictement plus grand
que"
 se lit
"inférieur
ou
égal à "ou
"plus petit ou
égal à " se lit
"inférieur
ou
égal à "ou
"plus petit ou
égal à "
 se lit
"supérieur
ou
égal à "ou
"plus grand ou
égal à " se lit
"supérieur
ou
égal à "ou
"plus grand ou
égal à "
Si je me
rappelle un peu de mes programmes antérieurs,
(je crois que c'est le programme de 5è), j'ai
déjà vu ces signes dans la leçon
sur les comparaisons et encadrement de nombres - Je me
rappelle :
Comparer les
nombrres 2,4 - 5,2 et 7 ; je peux écrire
:
2,4 <
5,2 < 7 ; je lis 2,4 plus petit que 5,2 plus
petit que 7
ou
encore : 7 > 5,2 > 2,4 ; je
lis : 7 plus grand que 5,2 plus grand que 2,4
ou
encore : faire un encadrement du
nombre 5,2 à 10-1: cela revient
à dire entre quels nombres à 1
chiffre après la virgule est compris 5,2 :
j'écris :
5,1 <
5,2 < 5,3 ; je lis 5,2 est compris entre 5,1
et 5,3 ; 5,2 est plus grand que 5,1 et plus
petit que 5,3
Règle : les signes des
inégalités impliquent toujour le plus
petit nombre du côté de la pointe du
signe (plus petit côté), et le plus grand
nombre du côté ouvrant du signe (+ grand
côté)
ex :
5,2 < 5,3 ou 5,3 > 5,2 : les 2 signes
utilisés sont différents, mais disent
exactement la même chose : 5,2 est plus petit
que 5,3 ou 5,3 est plus grand que5,2 : la
règle des signes est respectée : 5,2
se trouve dans les deux cas du côté de
la pointe du signe (plus petit côté)
et 5,3 du côté ouvrant du signe (+
grand côté).
Application des
inégalités à des  : :
 représentant
n'importe quelle valeur de nombre, je peux lui
appliquer des conditions d'inégalités
: représentant
n'importe quelle valeur de nombre, je peux lui
appliquer des conditions d'inégalités
:
ex :  < 2 < 2
Résoudre
l'inégalité reviendrait alors à
chercher la valeur de  inférieure à 2. Est-ce
qu'il existe une seule valeur de nombre
inférieure à 2 ? Bien sûr que non
! Je peux dire que 1 est inférieur à 2 ,
0 est inférieur à 2, -1 est
inférieur à 2 etc.... etc.....; et ceci
n'est que pour les nombres entiers ; je ne parle pas
des nombres décimaux..............Je peux alors
reprendre mon idée du départ, et dire
que si je devais résoudre cette
inégalité, j'aurais un ensemble de
solutions pour inférieure à 2. Est-ce
qu'il existe une seule valeur de nombre
inférieure à 2 ? Bien sûr que non
! Je peux dire que 1 est inférieur à 2 ,
0 est inférieur à 2, -1 est
inférieur à 2 etc.... etc.....; et ceci
n'est que pour les nombres entiers ; je ne parle pas
des nombres décimaux..............Je peux alors
reprendre mon idée du départ, et dire
que si je devais résoudre cette
inégalité, j'aurais un ensemble de
solutions pour  : c'est le principe même de
l'inéquation.
: c'est le principe même de
l'inéquation.
Je reprends mon
exemple ci-dessus :
Résoudre
l'inéquation  < 2 < 2
1ère
étape : je transcris mon
énoncé en français pour mieux
comprendre : on me demande de chercher les valeurs de
 inférieures
à 2 inférieures
à 2
Particularité du
signe :
< se lit strictement inférieur à : je
comprends et apprends les nuances et différences
entre les "strictement" et les "ou égal" :
|
Symboles
|
se lit
|
signifie
|
Représentation
|
<
>
|
strictement
inférieur à
strictement supérieur à
|
la
valeur butoire n'est pas
comprise dans les
solutions
|
crochet ouvrant :
]..............
|


|
inférieur ou
égal à
supérieur ou égal à
|
la
valeur butoire est
comprise dans les solutions
|
crochet fermant :
[..............
|
Je rectifie mon
énoncé : on me demande de chercher les
valeurs de  strictement inférieures
à 2 : c'est à dire que 2 ne sera pas
compris dans l'ensemble de mes solutions
strictement inférieures
à 2 : c'est à dire que 2 ne sera pas
compris dans l'ensemble de mes solutions
2ème
étape : je réfléchis
à mes solutions : toutes les valeurs
inférieures à 2 (2 exclus) seront solutions
pour  :
- 10 sera solution, - 125869 sera solution ..... :
- 10 sera solution, - 125869 sera solution .....
Jusqu'où vais-je trouver des solutions ? le
système numérique s'étend de moins
l'infini, (noté - ) en passant par 0, et
jusqu'à plus l'infini (noté + ) en passant par 0, et
jusqu'à plus l'infini (noté + ),
comme schématisé ci-dessous : ),
comme schématisé ci-dessous :
|
-
|
0
|
+
|
|
............................................
|
...|....
|
.................................................
|
Dire que la
solution de mon inéquation regroupe toutes les
valeurs inférieures à 2 (2 exclu des
solutions) - je vais donc prendre toutes les valeurs
correspondant à ce critère, et ce
jusqu'à - : j'écris
l'ensemble de mes solutions : : j'écris
l'ensemble de mes solutions :
S = ] - ; 2
[ ; 2
[
Je viens
d'écrire que l'ensemble des solutions de mon
inéquations va de moins l'infini à 2 exclus
: les crochets extérieurs ].....[ montrent que les
2 valeurs des extrémités sont exclues. De
toutes les façons, - et + et +  sont toujours exclues ;
.2 est également exclus , .....2 [ parce que
l'inéquation demande des valeurs strictement
inférieures à 2 sont toujours exclues ;
.2 est également exclus , .....2 [ parce que
l'inéquation demande des valeurs strictement
inférieures à 2
3ème
étape : je dois représenter
graphiquement l'ensemble de mes solutions. On me demande
souvent cet exercice après avoir résolu mon
inéquation. Méthode :
A la valeur 2,
je n'oublie pas de marquer le signe ....[ pour montrer
que cette valeur est exclue des solutions. Et
voilà, le tour est joué je viens de
résoudre ma première
inéquation.
Exercice N°
2 : Résoudre
l'inéquation : 2 - 3 +   3 - 5 3 - 5
Je me trouve en
présence d'une
inégalité composée de
différents calculs avec différents termes
dont au moins une
inconnue.
Les règles de calcul applicables sont celles que
je connais, et les méthodes et
propriétés pour l''isolation de l'inconnue
sont les mêmes que pour les équations.
Rappels :
 Pour résoudre une
équation je dois séparer mon inconnue
des autres termes de l'égalité :
règle : chaque fois que je passe un terme de
l'un ou de l'autre des côtés de
l'égalité, je change le signe de ce
terme : Même
chose pour les inéquations Pour résoudre une
équation je dois séparer mon inconnue
des autres termes de l'égalité :
règle : chaque fois que je passe un terme de
l'un ou de l'autre des côtés de
l'égalité, je change le signe de ce
terme : Même
chose pour les inéquations
Si a + b
- d
< c alors a < c -
b
+ d
ou
Si b - d < c + a alors b
- d
- c < a ( a >
b - d - c )
|
 Si a Si a  b = c alors b = c alors  ( c
÷ b ) : Même chose
pour les inéquations : ( c
÷ b ) : Même chose
pour les inéquations :
Si a  b < c alors b < c alors  ( c ÷ b ) ( c ÷ b )
|
La règle particulière
de l'inéquation :
si
-a < c alors a > - c ( ) )
si - b  a < c alors a > - a < c alors a > -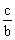
Cette règle est
systématique, et très importante : je dois
absolument la connaître. Je verrai un exemple
d'illustration dans l'exercice N° 3
Je reprends mon
exercice : Résoudre l'inéquation : 2 - 3 +
  3
- 5 3
- 5
1ère
étape : Comme en équation;
j'isole  dans la partie gauche de mon
équation, conformément à la
propriété énoncée ci-dessus,
et je passe tous les termes qui accompagnent dans la partie gauche de mon
équation, conformément à la
propriété énoncée ci-dessus,
et je passe tous les termes qui accompagnent  de l'autre
côté de l'égalité en changeant
leur signe : de l'autre
côté de l'égalité en changeant
leur signe :
2ème
étape : Tous les termes à droite
de ma parenthèse, sont des nombres , je peux
effectuer leur calcul :
   3 - 5 - 2 + 3 3 - 5 - 2 + 3
 3 - 5 - 2 + 3 = -1 3 - 5 - 2 + 3 = -1
 je peux écrire : je peux écrire :   -1 -1
j'ai résolu mon inéquation : je dois
maintenant en écrire les solutions :
j'interprète : les solutions de mon
inéquations représentent l'ensemble des valeurs
supérieures ou égales à
-1. Le
ou égal implique que la valeur butoire,
c'est-à dire -1 , soit solution de
l'inéquation (-1 fait partie de l'ensemble des
solutions) : Jusqu'où vais-je trouver des
solutions ? Je reprends le schéma du
système numérique et place ma valeur
butoire :
|
-
|
-1
|
0
|
+
|
|
............................................
|
...|..
|
...|....
|
.................................................
|
Dire que la
solution de mon inéquation regroupe toutes les
valeurs supérieures ou égales à -1
(- 1 inclus dans les solutions) revient à dire que
je pars de -1 et jusqu'à plus l'infini (+ ): j'écris
l'ensemble de mes solutions : ): j'écris
l'ensemble de mes solutions :
S = [ -1; + [ [
Je marque
l'appartenance du - 1 à l'ensemble de mes
solutions par le crochet fermé [.......Commme
d'habitude, +  se
termine par un crochet ouvert .........[ se
termine par un crochet ouvert .........[
3ème
étape : je dois maintenant
représenter graphiquement l'ensemble de mes
solutions : je suis les mêmes étapes que
dans l'exercice N° 1
1. Je reprends
le modèle de schéma du système
numérique, que j'ai représenté
ci-dessus avec -1, ma valeur butoire :
|
-
|
-1
|
0
|
+
|
|
............................................
|
..|..
|
...|....
|
.................................................
|
2. Je
délimite au stylo de couleur l'ensemble de mes
solutions : de -1 inclus à + : :
|
-
|
-1
|
0
|
+
|
|
............................................
|
..[.
|
...|....
|
.................................................
|
A la valeur
-1, je n'oublie pas de marquer le signe [.... pour
montrer que cette valeur est inclue dans les
solutions.
Exercice
N° 3 : Résoudre
l'inéquation : - 4 + 7 + + 7 +  > 3 - 5 + 4 > 3 - 5 + 4
1ère
étape : Comme tout à l'heure, et
comme pour les équations, je sépare les
termes en  des autres termes : je conserve
des autres termes : je conserve  du côté
gauche de mon égalité, (puisqu'il y est
déjà) et je passe tous les autres termes du
côté droit, en changeant leur signe ,
conformément à la propriété
que je connais : du côté
gauche de mon égalité, (puisqu'il y est
déjà) et je passe tous les autres termes du
côté droit, en changeant leur signe ,
conformément à la propriété
que je connais :
1. Je regroupe
mes termes en 
2. Je passe mes autres termes à droite de ma
parenthèse : 7 va devenir - 7
Je peux
écrire :
- 4 + +  > 3 - 5 + 4
- 7 > 3 - 5 + 4
- 7
2ème
étape : Tous les termes de même
nature sont regroupés de part et d'autre de mon
égalité, je vais pouvoir en effectuer le
calcul :
 - 4 - 4 +
+  = - 3
= - 3 ; conformément aux priorités de
calcul des termes en
; conformément aux priorités de
calcul des termes en 
 3 - 5 + 4 - 7 = -5 3 - 5 + 4 - 7 = -5
 je peux écrire : - 3 je peux écrire : - 3 > -5 > -5
Je
m'aperçois que je me retrouve avec une expression
sous la forme a  b > c b > c
- 3 = - 3 = - 3  
Comme pour une équation, je vais isoler  en faisant la
division de - 5 par - 3 en faisant la
division de - 5 par - 3
ATTENTION :
Je m'aperçois que pour isoler  , jevais diviser le
terme de l'autre côté de
l'inégalité par un nombre négatif :
j'applique la règle correspondante : si mon
incommue est négative ( , jevais diviser le
terme de l'autre côté de
l'inégalité par un nombre négatif :
j'applique la règle correspondante : si mon
incommue est négative (  -1 ou par tout autre nombre) : pour
l'isoler, je divise l'autre terme de mon
inégalité par ce nombre négatif,
et je
change le sens de mon inégalité. Je vais
alors écrire : -1 ou par tout autre nombre) : pour
l'isoler, je divise l'autre terme de mon
inégalité par ce nombre négatif,
et je
change le sens de mon inégalité. Je vais
alors écrire :
 < <  en divisant - 5
par - 3 , je change le sens de
l'inégalité en divisant - 5
par - 3 , je change le sens de
l'inégalité
 < <
j'ai
résolu mon inéquation : je dois maintenant
en écrire les solutions : j'interprète :
les solutions de mon inéquations
représentent l'ensemble des valeurs strictement
inférieures à  Le strictement implique que la
valeur butoire, c'est-à dire Le strictement implique que la
valeur butoire, c'est-à dire  , soit exclue de l'ensemble des
solution de l'inéquation : Jusqu'où vais-je
trouver des solutions ? Je reprends le schéma du
système numérique et place ma valeur
butoire : , soit exclue de l'ensemble des
solution de l'inéquation : Jusqu'où vais-je
trouver des solutions ? Je reprends le schéma du
système numérique et place ma valeur
butoire :  est > 0 puisque est > 0 puisque
  1,666666..... 1,666666.....
|
-
|
0
|

|
+
|
|
............................................
|
...|....
|
......|.......
|
.......................................
|
Dire que la
solution de mon inéquation regroupe toutes les
valeurs strictement inférieures à
 ( ( exclus des solutions)
revient à dire que je pars de exclus des solutions)
revient à dire que je pars de  et vais jusqu'à moins
l'infini (- et vais jusqu'à moins
l'infini (- ):
j'écris l'ensemble de mes solutions : ):
j'écris l'ensemble de mes solutions :
S = ] - ; ;
 [ [
Je marque
l'exclusion de  de l'ensemble de mes
solutions par le crochet ouvert.......[ Commme
d'habitude, de l'ensemble de mes
solutions par le crochet ouvert.......[ Commme
d'habitude,
-  commence par
un crochet ouvert ]....... commence par
un crochet ouvert ].......
3ème
étape : je dois maintenant
représenter graphiquement l'ensemble de mes
solutions :
1. Je reprends
le modèle de schéma du système
numérique, que j'ai représenté
ci-dessus avec  , ma valeur butoire
: , ma valeur butoire
:
|
-
|
0
|

|
+
|
|
............................................
|
...|....
|
......|.......
|
.......................................
|
2. Je
délimite au stylo de couleur l'ensemble de mes
solutions : de  exclus à - exclus à -
 : :
|
-
|
0
|

|
+
|
|
............................................
|
...|..
|
...[......
|
.......................................
|
A la valeur
 , je n'oublie pas de marquer le
signe....[ pour montrer que cette valeur est exclue
des solutions. , je n'oublie pas de marquer le
signe....[ pour montrer que cette valeur est exclue
des solutions.
Exercice N° 4: Inéquations et
fractions
Comme pour les équations, pour résoudre une
inéquation avec des fractions, je dois d'abord me
débarasser des dénominateurs. Pour cela, je
dois mettre absolument tous les termes de mon
inéquation sous le même dénominateur.
(revoir fiche les équations pour le
principe)
Résoudre
l'inéquation : 3 - -  
  + + 
1ère étape
: Je
mets tous les termes de mon inéqiation sous le
même dénominateur : les
dénominateurs existants : 2 et 4 : je recherche
un dénominateur commun : 4
 Je vais donc mettre tous les termes de
mon equation sur 4 : Je vais donc mettre tous les termes de
mon equation sur 4 :
3 (dénominateur 1) : Pour faire 4 , je dois
multiplier le dénominateur par 4 , je vais donc
également multipier mon numérateur par 4
: 3
(dénominateur 1) : Pour faire 4 , je dois
multiplier le dénominateur par 4 , je vais donc
également multipier mon numérateur par 4
: 3 =
= 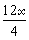
-  : Pour faire 4 , je
dois multiplier le dénominateur par 2, je vais
donc également multipier mon numérateur
par 2 : - : Pour faire 4 , je
dois multiplier le dénominateur par 2, je vais
donc également multipier mon numérateur
par 2 : -  = - = - 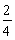 
 : Le dénominateur est
déjà 4 , je ne modifie pas la
fraction : Le dénominateur est
déjà 4 , je ne modifie pas la
fraction
 : (dénominateur 1) : Pour faire 4
, je dois multiplier le dénominateur par 4 , je
vais donc également multipier mon
numérateur par 4 : : (dénominateur 1) : Pour faire 4
, je dois multiplier le dénominateur par 4 , je
vais donc également multipier mon
numérateur par 4 :  = = 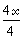
 Tous les termes de mon inéquation
sont sur 4, je réécris mon expression
modifiée : Tous les termes de mon inéquation
sont sur 4, je réécris mon expression
modifiée :
2ème étape
:
Tous les termes de mon inéquation sont
maintenant sous le même dénominateur :
conformément à la règle que je
connais, je vais pouvoir les supprimer. Mon
inéquation devient :
 Je retombe sur une inéquation
normale, sans dénominateur : je vais la
résoudre comme toutes les autres : Je retombe sur une inéquation
normale, sans dénominateur : je vais la
résoudre comme toutes les autres :
 Je sépare les termes en Je sépare les termes en  d'un
côté de l'égalité et les
autres termes de l'autre côté, en
changeant les signes de chacun des termes que je
change de côté : d'un
côté de l'égalité et les
autres termes de l'autre côté, en
changeant les signes de chacun des termes que je
change de côté :
 Je fais le calcul des x
conformément aux priorités de
calcul des termes en Je fais le calcul des x
conformément aux priorités de
calcul des termes en 
 je peux écrire : 6 je peux écrire : 6  3 3
    (3 ÷ 6) (3 ÷ 6)
    ou 0,5 ou 0,5
j'ai
résolu mon inéquation : je dois maintenant
en écrire les solutions : j'interprète :
les solutions de mon inéquations
représentent l'ensemble des valeurs
inférieures ou égales à
 Le
"ou égal" implique que la valeur butoire,
c'est-à dire Le
"ou égal" implique que la valeur butoire,
c'est-à dire  , soit inclue dans
l'ensemble des solution de l'inéquation :
Jusqu'où vais-je trouver des solutions ? Je
reprends le schéma du système
numérique et place ma valeur butoire : , soit inclue dans
l'ensemble des solution de l'inéquation :
Jusqu'où vais-je trouver des solutions ? Je
reprends le schéma du système
numérique et place ma valeur butoire :  est > 0 puisque
est > 0 puisque  = 0,5 = 0,5
|
-
|
0
|

|
+
|
|
............................................
|
...|....
|
......|.......
|
.......................................
|
Dire que la
solution de mon inéquation regroupe toutes les
valeurs inférieures ou égales à  (
( inclus dans les solutions) revient à
dire que je pars de inclus dans les solutions) revient à
dire que je pars de  et vais jusqu'à
moins l'infini (- et vais jusqu'à
moins l'infini (- ): j'écris
l'ensemble de mes solutions : ): j'écris
l'ensemble de mes solutions :
S = ] - ; ;  ] ]
Je marque
l'appartenance de  à l'ensemble de
mes solutions par le crochet fermé .......] Commme
d'habitude, à l'ensemble de
mes solutions par le crochet fermé .......] Commme
d'habitude,
-  commence par
un crochet ouvert ]....... commence par
un crochet ouvert ].......
3ème
étape : je dois maintenant
représenter graphiquement l'ensemble de mes
solutions :
1. Je reprends
le modèle de schéma du système
numérique, que j'ai représenté
ci-dessus avec  , ma valeur butoire
: , ma valeur butoire
:
|
-
|
0
|

|
+
|
|
............................................
|
...|....
|
......|.......
|
.......................................
|
2. Je
délimite au stylo de couleur l'ensemble de mes
solutions : de  inclus à - inclus à -
 : :
|
-
|
0
|

|
+
|
|
............................................
|
...|..
|
......].....
|
.......................................
|
A la valeur
 , je n'oublie pas de marquer le
signe....] pour montrer que cette valeur fait partie
des solutions. , je n'oublie pas de marquer le
signe....] pour montrer que cette valeur fait partie
des solutions.
Le principe de résolution d'une inéquation
n'est pas dur en lui même, puisque dans le principe
du calcul, il rejoint exactement le principe de
résolution des équations. Ce qu'il faut
bien comprendre surtout, c'est l'interprétation
des solutions.
|
Les
systèmes d'inéquations
|
On peut me demander certaines fois de résoudre un
système d'inéquations. Qu'est-ce que c'est
? C'est un ensemble d'au moins 2 inéquations
à résoudre. La particularité du
système ? L'ensemble des solutions du
système est l'interserction des solutions des 2
équations à résoudre.
1ère
étape : Je résouds mes
inéquations chacune séparément :
Les inéquations choisies ont déjà
été résolues respectivement dans les
exercices N° 1 et 3 ci-dessus. Je recopie leur
résolution :
2ème
étape : Je résouds maintenant
mon système d' inéquations : comme je vous
l'ai dit plus haut, les solutions de mon système
correspondent aux solutions communes à mes 2
inéquations. Pour y voir plus clair, je
représente les solutions de chacune des 2
inéquations. Mais cette fois, je les
représente sur le même schéma
:
des solutions :
1. Je reprends
le modèle de schéma du système
numérique, que j'ai représenté
ci-dessus et j'y inscrits les 2 valeurs butoires, pour
mes 2 inéquations : la 1ère = - 1 ; la
2è = 
|
-
|
-1
|
0
|

|
+
|
|
............................................
|
....|...
|
...|....
|
......|......
|
.......................................
|
2. Je
délimite au stylo de couleur l'ensemble des
solutions de mes 2 inéquations :
a. La
1ère en vert : de -1 inclus à +
b. La 2ème en orange : de  exclus à - exclus à -  : :
|
-
|
-1
|
0
|

|
+
|
|
............................................
|
...[..
|
...|....
|
......|......
|
.......................................
|
|
.........................................
|
....|...
|
...|...
|
.....[....
|
.......................................
|
3. Je
regarde sur le graphique quelle est la partie commune
aux solutions des 2 équations : quelle est la
partie du schéma qui est
délimitée à la fois par le vert
et le orange ? c'est la partie :
- 1  
C'est donc
cette partie qui sera solution de mon système
d'inéquations. J'écris :
Je regarde
si les valeurs extrêmes de mon intervalle
commune vont être solution ou non du
système ?
-1 est
solution de la 1ère inéquation : le
crochet fermant le montre
- 1 est également solution de la 2è
inéquation puisque les solutions vont de
 à - à - 
 -1 fera donc partie des solutions de mon
système -1 fera donc partie des solutions de mon
système
 est solution de la 1ère
inéquation puisque les solutions vont de
-1
à + est solution de la 1ère
inéquation puisque les solutions vont de
-1
à +
 n'est pas solution de la
2ème inéquation : le crochet ouvrant le
montre n'est pas solution de la
2ème inéquation : le crochet ouvrant le
montre
  ne fera donc pas
partie des solutions de mon système : la valeur ne fera donc pas
partie des solutions de mon système : la valeur
 est ecxlue est ecxlue
Je peux
maintenant écrire l'ensemble des solutions de
mon système :
S = [ -1;
 [ [
Nous avons vu dans la fiche sur les équations, que
les équations permettaient de résoudre
certains problèmes. Comment ? Par la mise en
équation des données du problème,
tout simplement.
Et bien nous allons voir maintenant que les
inéquations permettent aussi de résoudre
certains problèmes tout du moins certaines parties
de problèmes. Et oui, il n'y a pas de raison
!Voyons comment ça marche !
Exemple de
problème : (Brevet Clermont Ferrand -
Juin 2000):
[ La
société ALO propose un abonnement
téléphonique de 98 F par mois et 1,30 F par
minute de communication. La societé LAO propose un
abonnement téléphonique de 95 F par mois et
1,45 F par minute de communication. On désigne par
x le nombre de minutes de communication par mois .
1. Exprimer en
fonction de  le montant d'une facture de ALO, puis le montant d'une
facture de LAO
le montant d'une facture de ALO, puis le montant d'une
facture de LAO
2. Pour quelle durée de communication
mensuelles a-t-on interêt à choisir ALO ?
]
Résolution du problème :
Méthode :
1ère étape : Comme pour les
équations, puisque je vais résoudre ce
problème grâce à une
inéquation, je dois toujours commencer par
définir mon inconnue. Ici , c'est très facile
puisqu'on me nomme cette inconnue dans
l'énoncée : "On désigne par x le nombre
de minutes de communication par mois ."
 Soit Soit  le nombre de minutes de
communication par mois le nombre de minutes de
communication par mois
2ème
étape : Je comprends mon
problème et isole les éléments qui
vont me permettre de le résoudre. Ensuite,
j'essaie d'interpréter les données, et les
retranscrire en écriture
mathématique
Qu'est-ce qu'on
me dit ?
a / J'ai le
choix entre 2 formules de communication :
La 1ère
: Société ALO  abonnement 98 F + 1,30 F /mm de
communication. abonnement 98 F + 1,30 F /mm de
communication.
La 2ème : Société LAO  abonnement 95 F + 1,45 F /mm de
communication. abonnement 95 F + 1,45 F /mm de
communication.
Concrètement, cela veut
dire quoi ? Si j'ai posé  le nombre de minutes
de communication par mois, je peux maintenant
retranscrire chacune des 2 formules en écriture
mathématique : le nombre de minutes
de communication par mois, je peux maintenant
retranscrire chacune des 2 formules en écriture
mathématique :
ALO  98 + 1,30 98 + 1,30   : 98 + 1,30 : 98 + 1,30
LAO
 95 + 1,45 95 + 1,45   : 95 + 1,45 : 95 + 1,45
Je viens de
retranscrire l'énoncé de mon
problème en fonction de  , l'inconnue que j'ai posé : cela
tombe bien, car je m'aperçois que, grâce
à mon raisonnement logique je viens de
répondre à la première question du
problème. Me guideraient-ils dans mes
démarches ? Sans aucun doute !!! , l'inconnue que j'ai posé : cela
tombe bien, car je m'aperçois que, grâce
à mon raisonnement logique je viens de
répondre à la première question du
problème. Me guideraient-ils dans mes
démarches ? Sans aucun doute !!!
3ème
étape : je tente de comprendre la
question du problème (2.). Qu'est-ce qu'on me
demande ? Pour quelle durée de communication
mensuelles a-t-on interêt à choisir ALO ?
C'est à dire, si  le nombre de minutes de
communication par mois, Pour quelle valeur de le nombre de minutes de
communication par mois, Pour quelle valeur de ai-je
intérêt à choisir ALO, c'est à
dire la première formule. ai-je
intérêt à choisir ALO, c'est à
dire la première formule.
Je resitue le problème : j'ai 2 formules et on me
demande jusqu'à combien de minutes je pourrai
téléphoner avec la 1ère formule, et
que cela me revienne moins cher que la deuxième :
je dois donc comparer les 2 formules : je pose :
98 + 1,30 < 95 + 1,45 < 95 + 1,45
La mise en
inégalité de mes 2 formules va me permettre
de déterminer pour quelles valeurs de x la
première formule est plus avantageuse que la
deuxième (c'est à dire inférieure
à). Pourquoi ai-je choisi le "strictement" ? Tout
simplement parce que si j'avais choisi le "ou
égal", ma valeur butoire de  aurait convenu aussi
bien pour la 1ère que pour la 2è (valeur
butoire = 2ème formule aussi avantageuse que la
1ère). Or ce n'est pas tout à fait ce qu'on
me demande : aurait convenu aussi
bien pour la 1ère que pour la 2è (valeur
butoire = 2ème formule aussi avantageuse que la
1ère). Or ce n'est pas tout à fait ce qu'on
me demande :
4ème
étape : Je résouds
l'inéquation :
5ème
étape : je restitue le résultat
de mon inéquation dans le contexte de mon
problème : si  représente le nombre de
minutes de communication par mois, cela veut dire que le
nombre de minutes de communication doit être
strictement supérieur à 20 pour que la
formule ALO soit plus avantageuse que la formule LAO. Par
conséquent, je réponds à la question
de mon problème par une phrase en français
: représente le nombre de
minutes de communication par mois, cela veut dire que le
nombre de minutes de communication doit être
strictement supérieur à 20 pour que la
formule ALO soit plus avantageuse que la formule LAO. Par
conséquent, je réponds à la question
de mon problème par une phrase en français
:
J'ai
intérêt de choisir la formule ALO à
partir de 21 minutes de communication
mensuelle.
Mon
problème est terminé.
NB : Comme pour
les problèmes avec des équations, je
vérifie quand même la cohérence de
mon résultat dans l'autre sens :
20 minutes
étant ma valeur butoire, je regarde si
effectivement les 2 formules me couteront le même
prix pour ce temps de communication :
ALO  98 + 1,30 98 + 1,30  20 : 98 + 26 = 124 20 : 98 + 26 = 124
LAO
 95 + 1,45 95 + 1,45  20 : 95 + 29 = 124 20 : 95 + 29 = 124
Mon
raisonnement est juste : pour 20 minutes de communication
mensuelle, les 2 formules me coutent le même prix,
soit 124 F. Essayons maintenant avec des valeurs
supérieures à 20 mn : !
|
|
ALO
|
LAO
|
|
21 mm
|
98 + 1,30  21 : 98 + 27,30 =
125,30
21 : 98 + 27,30 =
125,30
|
95 + 1,45  21 : 95 + 30,45 =
125,45
21 : 95 + 30,45 =
125,45
|
|
25 mn
|
98 + 1,30  25 : 98 + 32,50 =
130,50
25 : 98 + 32,50 =
130,50
|
95 + 1,45  25 : 95 + 36,25 =
131,25
25 : 95 + 36,25 =
131,25
|
|
30 mn
|
98 + 1,30  30 : 98 + 39 =
137,00 30 : 98 + 39 =
137,00
|
95 + 1,45  30 : 95 + 43,50 =
138,50
30 : 95 + 43,50 =
138,50
|
|
etc....
|
|
|
Mon
résultat semble se vérifier : pour toutes
les communications supérieures à 20 mn, les
communications avec ALO me couteront moins cher qu'avec
LAO. Mon problème doit être correctement
résolu !!!!
IMORTANT : les problèmes devant se
résoudre au moyen d'inéquations sont
toujours construits sur le même principe : si on me
demande de comparer 2 formules de choix, ou si on me
demande laquelle est plus avantageuse ou à partir
de quelle valeur, cela doit me mettre la puce à
l'oreille ! J'utiliserai exactement la même
méthode que ce problème d'exemple pour le
résoudre. Facile non ????
|
