REPERE, COORDONNEES, DISTANCES & VECTEURS

2 S'quizzes disponibles

S'quizz n° 2

	Contenu : 12 questions à choix multiple Objectif : Vérifier que je sais faire des calculs dans le repère à partir de coordonnées de points Principe : Trois propositions de réponse : une seule est correcte ; à moi de trouver laquelle dans chacun des cas proposés

	Questions Résultats
	Question n° 1 Dans le repère, O,I, J, soit A(2 ; 4) et B(-1 ; -2) : quelle est la distance AB ? 45 45 9     Question n° 2   Dans le même repère, j'ajoute un point C de coordonnées x = 4 et y = - 3 : quelle sera alors la distance OC ? 5 cm 0 1 cm     Question n° 3   Dans un repère, j'ai placé 3 points : E (-4 ; 3), F (0 ; 2) et G (4 ; 1) : F est-il le milieu du segment [EG] ? Oui, je le vois quand je trace le repère et place les points Oui, ses coordonnées sont effectivement celles du milieu de [EG] Non, car du point F on trace une droite parallèle à l'axe des abscisses     Question n° 4   Quelle est la formule de calcul justement des coordonnées de I milieu du segment [AB] ? 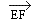: I (;) l I (distance AB / 2) I ()       Question n° 5   (2 ; - 3) : (-2 ; 3) Ces 2 vecteurs : Sont égaux Sont opposés N'ont rien en commun       Question n° 6   On me donne les coordonnées du vecteur : (4 ;7) : avec ces coordonnées, je peux : Trouver les coordonnées des points A et D Trouver seulement les coordonnées du point A Trouver ni les coordonnées du point A, ni les coordonnées du point D       Question n° 7   : (6 ; - 3) et S (2,5; 1) Quelles sont les coordonnées du point E ? E (-3,5 ; -4) E (3,5 ; - 4) E (5 ; - 5,5)       Question n° 8   (7 ; - 2) (7 ; - 2) Ces 2 vecteurs : Sont égaux Sont opposés N'ont rien en commun       Question n° 9   Pour ces mêmes vecteurs, le quadrilatère KGDA est un : rectangle parallèlogramme quadrilatère quelconque     Question n° 10   J'ai placé les points A(1 ; 7), B (4 ;:5), C (4 ; 1) et D (7 ; - 1) : le quadrilatère ABDC est un parallèlogramme : pourquoi ? Je le vois en plaçant les points dans mon repère et en traçant la figure Les distances AB, CD, AC et BD sont de même mesure respectivement 2 à deux Les vecteurs AB et CD sont égaux       Question n° 11   Dans mon repère, je veux former un parallèlogramme avec mes points, C,D,E,F : j'ai C (1 ;3), D (4 ; -1), et F (-2 ; -2) : où sera placé mon point E ? (- 1 ;2) (-5 ; 2) (2 ; 2)       Question n° 12   Dans le repère O, I, J, je place 3 points D,E, et F : le triangle DEF formé par ces 3 points est rectangle : pourquoi ? J'ai calculé les coordonnées des vecteurs D,E, et F, et j'obtiens : vecteur D = vecteur E = vecteur F J'ai calculé les distances DE, DF et EF et j'obtiens : DE2 + DF 2 = EF 2 Le triangle DEF est rectangle car les points forment des angles droits avec le quadrillage du repère

	Résultats :
	Le test est à présent terminé : Relis bien tes réponses avant de continuer Pas d'erreurs ? Alors tu peux maintenant vérifier les résultats et obtenir ta note : Note obtenue : Alors ?? Un conseil : si tu as obtenu moins de 10 sur 12 à ce test, tu ne maîtrises pas suffisamment les points importants du chapitre : Révise par conséquent la fiche d'explication correspondante !! Et refais le test, pour vérifier que tu as mieux compris .... Fiche d'explication sur le repère I Fiche d'explication sur le repère II | Refaire le test | Regarde bien également les questions pour lesquelles tu as fait des erreurs : Tu peux également vérifier les bonnes réponses :