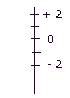|
LES NOMBRES RELATIFS
|

|
|
Qu'est-ce
qu'un nombre relatif ?
|
Ce sont les
nombres qui comportent un signe : positif (+) ou
négatif (-) par rapport à zéro.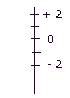
Règle : tous les nombres
négatifs (signe - ) sont inférieurs à
zéro - Tous les nombres positifs (signe + ) sont
supérieurs à zéro
Les nombres
relatifs sont composés d'un signe : + ou - et
d'une
valeur absolue : la valeur absolue d'un nombre
relatif peut être un nombre entier, décimal,
une racine carrée un terme en  , y,....ou une fraction , y,....ou une fraction
Exemples
:
(-36) ; (+ 12,35)
; (+ 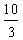 ) ; (+ ) ; (+  39) 39)
36 ; 12,35 ; 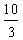 ; ; 39 et sont les valeurs absolues des
nombres relatifs ci-dessus 39 et sont les valeurs absolues des
nombres relatifs ci-dessus
|
A savoir : Opposé d'un
nombre : l'opposé
d'un nombre, c'est le nombre qui a la même
valeur absolue, mais est de signe contraire
Exemple :
2 (ou + 2) et - 2
Règle :
L'addition de deux nombres
opposés est toujours égale à
0
2 + (-2) = 2 - 2 = 0 (je
prends 2 et j'enlève 2 )
|
|
Opérations avec les
nombres relatifs
|
La présence de signes devant les nombres, imposent
une règle spécifique de calcul des signes,
qu'il faut savoir par coeur : par contre les signes ne
modifient en rien les règles de calcul vues dans
les différentes rubriques sur les
propriétés des opérations et
opérations avec les différents termes (voir
rubriques correspondantees)
J'apprends la
règle des signes, et je m'entraîne
beaucoup pour ne plus me tromper : car les signes sont
partout !!!
(équations, développement, fractions
.....)
|
J'ai deux
nombres positifs
|
|
Opération
|
signe du
résultat
|
Méthode de
calcul
|
|
Addition
|
+
|
les valeurs absolues des
nombres s'ajoutent
(+
3,7) + (+ 4,8) = + (3,7 + 4,8) =
+ 8,5
|
|
Soustraction
|
|
|
|
si la
valeur absolue du 1er nombre est
supérieur à celle du
2è
|
+
|
les valeurs absolues des nombres se
soustraient
(+
4,8) - (+ 3,7) = + (4,8 - 3,7) =
+ 1,1
car 4,8 > 3,7
|
|
Si la
valeur absolue du 1er nombre est
inférieure à celle du
2è
|
-
|
les valeurs absolues des nombres se
soustraient
(+ 3,7) - (+ 4,8) =
- (4,8 - 3,7) =
- 1,1
car 3,7 < 4,8
|
|
Multiplication
|
+
|
les valeurs absolues des nombres se
multiplient
(+ 3,7)  (+ 4,8) =
+ (3,7 (+ 4,8) =
+ (3,7  4,8) =
+ 17,76 4,8) =
+ 17,76
|
|
Division
|
+
|
les valeurs absolues des nombres se
divisent
(+
3,7) ÷
(+ 4,8) =
+ (3,7 ÷ 4,8) =
+ 0,77
|
|
J'ai deux
nombres négatifs
|
|
Opération
|
Signe du
résultat
|
Méthode de
calcul
|
|
Addition
|
-
|
les valeurs absolues des nombres s'ajoutent
(- 3,7) + (- 4,8) =
- (3,7 + 4,8) =
- 8,5
|
|
Soustraction
|
le signe
sera celui du nombre qui possède la plus
grande valeur absolue
|
la soustraction se
transforme en addition d'un nombre
positif;
- (-....) = + ; la
règle devient alors celle de l'addition
d' un nombre positif et un nombre négatif
: les valeurs
absolues des nombres se soustraient
(- 3,7) - (- 4,8) =
(- 3,7) +
4,8 =
+ 1,1
car 4,8 > 3, 7, et 4,8 est positif
(- 4,8) - (- 3,7) =
(- 4,8) +
3,7 =
- 1,1
car 4,8 > 3, 7, et 4,8 est
négatif
|
|
Multiplication
|
+
|
les valeurs absolues des
nombres se
multiplient
(- 3,7)  (-
4,8) = + (3,7 (-
4,8) = + (3,7  4,8) =
+ 17,76 4,8) =
+ 17,76
|
|
Division
|
+
|
les valeurs absolues des nombres se divisent
(- 3,7) ÷ (- 4,8) =
+ (3,7 ÷ 4,8) = + 0,77
|
|
J'ai un
nombre positif et un nombre
négatif
|
|
Opération
|
signe du
résultat
|
Méthode de
calcul
|
|
Addition
|
le signe
sera celui du nombre qui possède la plus
grande valeur absolue
|
les valeurs absolues des
nombres se soustraient
(+ 3,7) + (- 4,8) =
- (4,8 + 3,7) =
- 1,1
Explication : 4,8 est la
plus grande valeur absolue, le signe du
résultat est donc négatif
(- 3,7) + (+ 4,8) = +
(4,8 -
3,7) =
+ 1,1
car 4,8 > 3, 7, et 4,8 est positif
|
|
Soustraction
|
|
|
|
Si un nombre de signe
positif soustrait un nombre de signe
négatif :
|
+
|
la soustraction se
transforme en addition d'un nombre
positif; on
retrouve le
- (-....) = + ; la
règle devient alors celle de l'addition
de deux nombres positifs : les valeurs absolues
des nombres s'ajoutent
(+ 4,8) - (- 3,7) =
(+ 4,8) +
3,7 = + (4,8 + 3,7) =
+ 8,5
|
|
Si un nombre de signe
négatif soustrait un nombre de signe
positif :
|
-
|
la soustraction se transforme en addition de
deux nombres négatifs : les valeurs
absolues des nombres s'ajoutent
(-
3,7) - (+ 4,8) = - 3,7 - 4,8 =
- 8,5
|
|
Multiplication
|
-
|
les valeurs absolues des nombres se
multiplient
(+ 3,7)  (-
4,8) = - (4,8 (-
4,8) = - (4,8  3,7) =
- 17,76 3,7) =
- 17,76
|
|
Division
|
-
|
les valeurs absolues des nombres se divisent
(+
3,7) ÷
(- 4,8) =
- (3,7 ÷ 4,8) = - 0,77
(- 3,7) ÷
(+ 4,8) =
- (3,7 ÷ 4,8) = - 0,77
|
IMPORTANT : par
définition, un nombre qui ne possède pas de
signe est un nombre positif
Ex : 2x - 3 x revient à faire
(+
2x) - (+ 3x) ; je
suis donc en présence d'une soustraction de
nombres positifs
Remarque : Quand j'ai bien pris
l'habitude des opérations avec les signes, je peux
résumer les opérations de la façon
suivante :
En addition et soustraction :
2 signes + donnent un signe + ;
addition des nombres
2 signes - donnent un signe - ; addition des
nombres
1 signe + et un signe - : donnent un + quand le + a la
plus grande valeur absolue; sinon ils donnent un - ;
soustraction des nombres
- (-....) = +
En multiplication :
+ par + = +
- par - = +
+ par - = -
En division :
+ sur + = +
- sur - = +
+ sur - ou - sur + = -
Je peux ainsi considérer que l'expression
:
2x - 3 x est l'addition d'un nombre
positif et d'un négatif : je
réagis : un + et un - donnent un + quand le + a
la plus grande valeur absolue; sinon ils donnent un -
:
2x - 3 x = - x
Je peux aussi me dire que si
j'enlève trois à deux, j'aurai
forcément un résultat inférieur
à 0 donc négatif : si j'enlève 2
à 2 j'btiendrai 0 ; si j'enlève 3 à
2 j'obtiendrai -1
|